Vi siete mai chiesti quanti sono i numeri?
Questo laboratorio è stato sviluppato da Francesca Arcese, Roberta Befera, Andrea Buzzacco, Sofia Corradetti, Ludovica Fiori, Alessandra Todesca in collaborazione con Donato Bini (CNR-IAC), il progetto è stato coordinato da Gualtiero Grassucci (lss G.B. Grassi di Latina).
Materiale didattico a supporto
- Il fascicolo (in formato PDF di circa 10MB);
- La libreria di funzioni sviluppata con Blockly disponibile online su questo stesso blog;
- Procedure e funzioni in Python e XML (così come generata da Blockly, in formato ZIP).
Vi siete mai chiesti quanti sono i numeri? Infiniti: questa è la risposta!
I numeri possono essere: naturali, interi, razionali, reali o irrazionali. Noi abbiamo lavorato sui numeri irrazionali e in particolare sui numeri trascendenti. Ma, di preciso, cos’è un numero trascendente? I numeri trascendenti sono numeri irrazionali che non sono numeri algebrici e quindi, non sono soluzione di nessuna equazione polinomiale (con coefficienti interi o razionali).
Prerequisiti
Prima di iniziare il nostro laboratorio, è necessario:
- saper determinare una funzione che approssimi una serie di dati sperimentali;
- conoscere il concetto di derivata;
In alcuni casi è necessario utilizzare dei software CAS (Computer Algebra System), come Geogebra.
Obiettivi
L’obiettivo è costruire, in linguaggio naturale ma abbastanza rigoroso, procedure per approssimare numeri irrazionali (come radice quadrata di due) o trascendenti (come pi greco o il numero di Eulero e) e dare una stima della convergenza dei metodi trovati.
Obiettivo ulteriore è tradurre le procedure, scritte in linguaggio naturale, in un linguaggio di programmazione formale usando il generatore di codice Blockly. Blockly è un generatore di codice sviluppato da Google, open source, nato per facilitare l’apprendimento delle basi del coding e la robotica educativa. Unendo i blocchi di comando come i pezzi di un puzzle, si possono costruire funzioni via via più complesse.
La libreria
Contestualmente alla soluzione del problema, nel corso del laboratorio le funzioni realizzate sono state implementate mediante Blockly. Qui presentiamo la libreria e la sua struttura.
Approssimazione di numeri irrazionali e trascendenti
- Approssimazione si e mediante formula di Taylor: Taylor_e(iterazioni)
- Approssimazione di e mediante metodo di Newton: Newton_e(iterazioni)
- Approssimazione di pi greco mediante formula di Taylor: Taylor_PiAtan1(iterazioni), Taylor_PiAtan1-2_1-3(iterazioni)
- Approssimazione di radice di 2 mediante metodo di Newton: Newton_r2(iterazioni)
- Approssimazione della sezione aurea mediante metodo di Newton: Newton_phi(iterazioni)
- Approssimazione di un numero reale con il metodo del minimo scostamento: MinimoScostamento(ripetizioni, trascendente)
- Fattori primi usati nel metodo del minimo scostamento: MinimoScostamento(ripetizioni, trascendente)
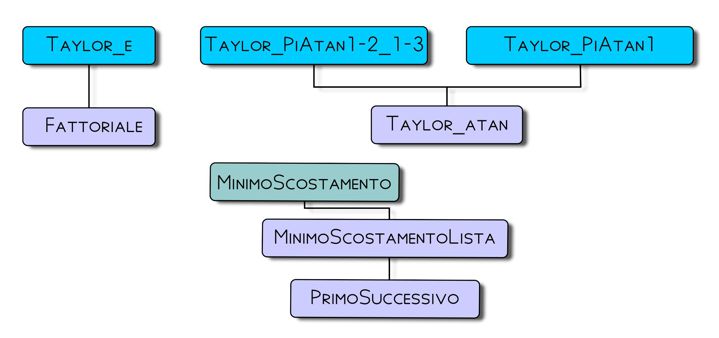
La struttura della libreria: approssimazione irrazionali e trascendenti. Le funzioni più in alto nella figura usano le funzioni più in basso a cui sono collegate. Per esempio: sia MinimoScostamento usa MinimoScostamentoLista che a sua volta usa PrimoSuccessivo. Le funzioni che approssimano con il metodo di Newton non usano nessun altra funzione.
Approssimazione del numero di Eulero e tramite serie di Taylor
Approssimazione mediante lo sviluppo in serie di Taylor, in un intorno di zero, della funzione esponenziale, sviluppo calcolato poi per x = 1:
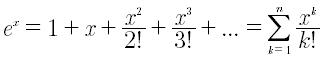
da cui:
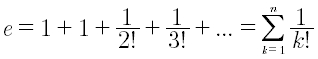
Taylor_e(iterazioni)
Dove iterazioni è il numero di iterazioni usato nello sviluppo in serie. Restituisce un numero reale.
Usa Fattoriale(x).
Approssimazione del numero di Eulero e con il metodo di Newton
Il numero di Eulero e è approssimato ricercando una soluzione numerica dell’equazione:
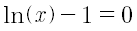
Newton_e(iterazioni)
Dove iterazioni è il numero di iterazioni usato nello sviluppo in serie. Restituisce un numero reale.
Approssimazione di pi greco tramite serie di Taylor
L’approssimazione è ottenuta sviluppando la funzione arcotangente in un intorno di zero e calcolando poi in un angolo opportuno.
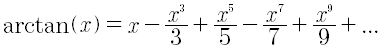
Taylor_PiAtan1(iterazioni)
Taylor_PiAtan1-2_1-3(iterazioni)
Dove iterazioni è il numero di iterazioni usato nello sviluppo in serie. Entrambe le funzioni restituiscono un numero reale.
La prima funzione calcola l’arcotangente in uno e moltiplica il risultato per quattro. La seconda utilizza la proprietà:
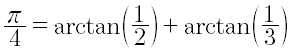
e quindi somma l’arcotangente di 1/2 e di 1/3 e moltiplica il risultato per quattro.
Usa Taylor_atan(iterazioni, x).
Approssimazione di radice di due con il metodo di Newton
L’approssimazione è calcolata applicando il metodo di Newton all’equazione:
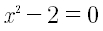
Newton_r2(iterazioni)Dove iterazioni è il numero di iterazioni usato nello sviluppo in serie. Restituisce un numero reale.
Approssimazione della sezione aurea con il metodo di Newton
L’approssimazione è calcolata applicando il metodo di Newton all’equazione:
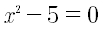
e l’approssimazione ottenuta è usata per calcolare la sezione aurea.
Newton_phi(iterazioni)Dove iterazioni è il numero di iterazioni usato nello sviluppo in serie. Restituisce un numero reale.
Approssimazione di un numero reale con il metodo del minimo scostamento
Il numero reale è approssimato come prodotto di razionali:
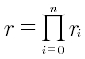
in cui il numeratore e il denominatore sono numeri primi scelti secondo la formula:
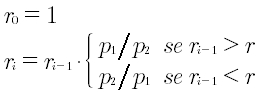
MinimoScostamento(ripetizioni, trascendente)Dove ripetizioni è il numero di iterazioni e trascendente il numero reale da approssimare. Restituisce un numero reale.
Usa MinimoScostamentoLista(ripetizioni, trascendente)
Fattori del prodotto usato nel metodo del minimo scostamento
Il metodo del minimo scostamento approssima un numero reale come prodotto di razionali, questa funzione costruisce una lista in cui il primo elemento è +1 o -1 a seconda del segno del numero da approssimare e gli elementi successivi sono numeratore e denominatore del razionale seguente.
MinimoScostamentoLista(ripetizioni, trascendente)Dove ripetizioni è il numero di iterazioni e trascendente il numero reale da approssimare. Restituisce una lista di interi.
Derivata aritmetica
- Derivata logaritmica: ld(x)
- Derivata di un numero intero: DAIntero(x)
- Derivata di un numero razionale: DARazionale(x)
- Derivata di un numero reale: DAReale(x)
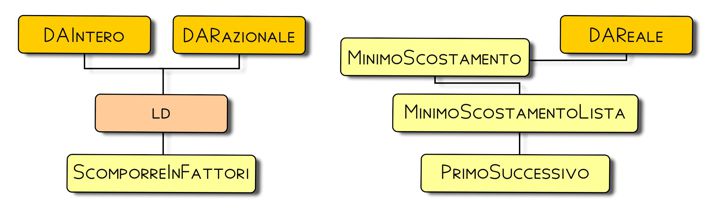
La struttura della libreria: derivata aritmetica. Le funzioni più in alto nella figura usano le funzioni più in basso a cui sono collegate. Per esempio: sia DAIntero che DARazionale usano ld che a sua volta usa ScomporreInFattori.
Derivata logaritmica
La derivata logaritmica, in analogia con la derivata classica, è definita come il rapporto tra la derivata n’ di un numero e il numero stesso:
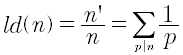
ld(x)Dove x è il numero intero di cui calcolare la derivata logaritmica. Restituisce un numero reale.
Usa ScomporreInFattori e PrimoSuccessivo.
Derivata di un intero
La derivata di un intero n è data dal numero stesso moltiplicato per la sua derivata logaritmica o, in altre parola, per la somma degli reciproci dei primi che dividono n.
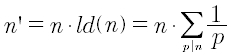
DAIntero(x)Dove x è il numero intero di cui calcolare la derivata aritmetica. Restituisce un numero intero.
Usa ld
Derivata di un razionale
La derivata di un numero razionale si ottiene calcolando innanzitutto la somma dei reciproci dei primi che dividono il numeratore meno la somma dei reciproci dei primi che dividono il denominatore e moltiplicando il risultato per il razionale stesso.
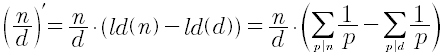
DARazionale(numeratore, denominatore)Dove numeratore è il numeratore del numero razionale da derivare e denominatore il denominatore dello stesso numero. Restituisce un numero reale.
Usa ld
Derivata di un numero reale
La derivata di un numero reale è ottenuta sviluppando il numero in un prodotto di frazioni, in cui numeratore e denominatore sono numeri primi, con il metodo del minimo scostamento e successivamente derivando il prodotto così ottenuto. Ovviamente il risultato dipende dall’estensione dello sviluppo.
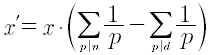
DAReale(x, iterazioni)Dove x è il numero reale da derivare e iterazioni il numero di iterazioni nello sviluppo del numero reale con il metodo del minimo scostamento. Restituisce un numero reale.
Usa DAIntero e MinimoScostamentoLista.