Un laboratorio tra onde gravitazionali e apprendimento strategico:
- ChatGPT come collaboratore 1/3 (questo articolo: Un esperimento didattico)
- ChatGPT come collaboratore 2/3 (Come gli studenti hanno usato – e guidato – l’AI)
- ChatGPT come collaboratore 3/3 (Cosa ci dicono le risposte degli studenti)
Un esperimento didattico
Tra scienza, tecnologia e autonomia
Cosa succede quando a una classe di liceo scientifico si propone un problema reale di fisica teorica – tratto da un articolo di ricerca pubblicato su Physical Review – e si affida il compito di esplorarlo a studenti che non conoscono né l’argomento né le tecniche necessarie per risolverlo? E se al loro fianco, come supporto, ci fosse un’intelligenza artificiale generativa?
Questa è l’idea alla base del laboratorio Onde gravitazionali 3, sperimentato nella primavera 2025 in una terza classe del Liceo Scientifico G.B. Grassi di Latina. Il laboratorio, parte delle attività del programma Research in Action ha proposto a ragazze e ragazzi un’attività di modellizzazione matematica basata su un problema autentico fornito dal prof. Donato Bini (IAC-CNR), ispirato all’articolo Beyond the geodesic approximation di Barack e Sago.
Nel dettaglio, il laboratorio è stato proposto a una classe terza del liceo scientifico G.B. Grassi di Latina, 25 alunni e alunne in tutto, che è parte del progetto Liceo matematico della scuola. Al termine dell’anno scolastico le valutazioni finali di studenti e studentesse sono state:
| Valutazione /10 | Matematica | Fisica | Verifica del laboratorio |
| 8 – 10 | 7 | 9 | 6 |
| 6 – 7 | 16 | 15 | 13 |
| 5 o meno | 2 | 1 | 6 |
Tempi: 12 ore tra aprile e maggio 2025.
Il problema
Trovare una funzione in due variabili da dati numerici reali
Il tema: stimare, a partire da una tabella di dati numerici, l’andamento di una funzione f(u, e) dove u = 1/p è una coordinata radiale ed e è l’eccentricità dell’orbita di un corpo che sta spiraleggiando intorno ad un altro a causa della mutua interazione gravitazionale tra i due. Gruppi differenti hanno affrontato il fit di funzioni diverse dipendenti dagli stessi dati. Un compito tutt’altro che scolastico, che richiedeva: analisi dati, comprensione di un contesto scientifico avanzato, costruzione di modelli approssimanti e valutazione della bontà del risultato (cfr. Beyond the geodesic approximation di Barack e Sago).

Obiettivi didattici
Autonomia, astrazione, strategia
L’obiettivo non era arrivare al risultato giusto, ma attivare strategie di risoluzione, fare ipotesi, usare strumenti matematici noti (come i polinomi) in contesti nuovi, visualizzare, verificare ma soprattutto collaborare con un’IA senza lasciarsi guidare passivamente.
L’attività prevedeva/richiedeva:
- l’analisi autonoma dei dati forniti;
- l’uso di ChatGPT come collaboratore (e non semplicemente tutor) e sparring partner;
- la modellizzazione tramite software CAS (xMaxima) e grafici 3D (GeoGebra);
- la costruzione e la valutazione di una funzione a due variabili f(u,e) coerente con i dati sperimentali.
L’intelligenza artificiale
Guida e partner
In linea con quanto discusso nell’articolo Beyond Answers – How LLMs Can Pursue Strategic Thinking in EducationBeyond Answers – How LL…, ChatGPT è stato presentato agli studenti non come uno che sa già la risposta, ma come collaboratore strategico in grado di:
- proporre approcci diversi a un problema;
- guidare nella scelta delle domande giuste;
- suggerire soluzioni, senza imporle;
- aiutare a ragionare sui risultati ottenuti.
Il laboratorio ha reso tangibile una delle idee chiave dell’articolo: l’LLM come alleato per esplorare, non per cercare scorciatoie. Una collaborazione in cui l’intelligenza artificiale diventa un’estensione del ragionamento umano, non un sostituto.
Uno sguardo al risultato finale
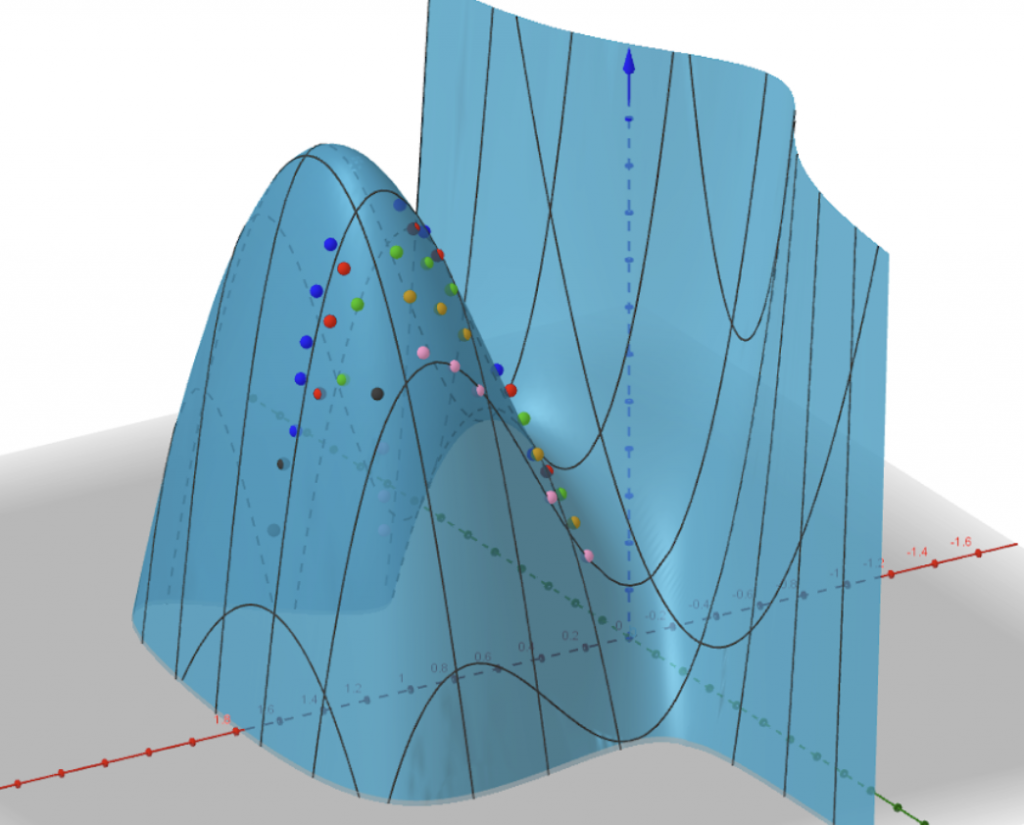
Senza anticipare troppo gli sviluppi dei prossimi articoli, vale però la pena accennare a ciò che uno dei gruppi di lavoro è riuscito a realizzare (un esempio tra gli altri). Partendo da un insieme di dati numerici ottenuti da simulazioni altamente specialistiche, un gruppo di studenti ha costruito – utilizzando GeoGebra, xMaxima e con il supporto di ChatGPT – una funzione in due variabili MΩr0(u,e) (una delle funzioni proposte nell’articolo di Barak e Sago) che approssima un potenziale gravitazionale corretto da effetti relativistici. Il modello finale, basato su interpolazioni polinomiali e pensato per essere semplice ma efficace, ha mostrato un errore medio accettabile (varianza ≈ 0.11) e una coerenza sorprendente con i dati forniti. Un risultato che dimostra come, anche partendo da un problema complesso e apparentemente fuori portata, sia possibile – con gli strumenti giusti – arrivare a una soluzione significativa e comprensibile.
La difficoltà principale del problema risiedeva nel fatto che la funzione obiettivo dell’approssimazione dipende da due variabili, u=1/p (la coordinata radiale) ed e (l’eccentricità orbitale). È bene ricordare che le funzioni a due variabili non sono un argomento che si affronta nel corso di matematica di un liceo scientifico. La strategia risolutiva adottata è stata quella di:
- rappresentare i dati in un sistema di riferimento tridimensionale e riconoscere eventuali regolarità;
- suddividere i dati in sottoinsiemi per valori fissati dell’eccentricità e;
- approssimare ciascun sottoinsieme con un polinomio di terzo grado in una sola variabile, u;
- integrare in una funzione unica f(u,e) i polinomi ottenuti, interpolando i coefficienti dei polinomi in funzione della variabile e (un possibile approccio era suggerito dal professor Bini nella proposta di attività).
In un’epoca in cui il sapere è sempre più accessibile, ci siamo chiesti: può un’intelligenza artificiale diventare una guida per esplorare territori della scienza troppo lontani per l’età degli studenti? Questo laboratorio ha provato a rispondere.
Nel prossimo articolo Come gli studenti hanno usato – e guidato – l’AI parleremo proprio del rapporto tra studenti e intelligenza artificiale: come è stata usata, con quali difficoltà, con quali intuizioni. E cosa abbiamo imparato osservandoli lavorare.