Nuovo anno, nuovi problemi
Questo articolo è stato scritto in collaborazione con Francesca Arcese, Roberta Befera, Andrea Buzzacco, Sofia Corradetti, Ludovica Fiori.
La libreria realizzata con Blockly si può trovare qui.
Vi siete mai chiesti quanti sono i numeri? Infiniti: questa è la risposta!
I numeri possono essere: reali, razionali, interi relativi, naturali o irrazionali.
A noi è stato chiesto di occuparci dei numeri irrazionali e in particolare dei numeri trascendenti. Ma, di preciso, cos’è un numero trascendente? I numeri trascendenti sono numeri irrazionali che non sono numeri algebrici e quindi, non sono soluzione di nessuna equazione polinomiale (con coefficienti interi o razionali).
Per esempio: radice quadrata di due è un numero irrazionale ma non è trascendente, perché è soluzione dell’equazione
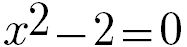
Infatti, isolando il termine di secondo grado in x si ha:
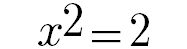
da cui, facilmente, le due soluzioni dell’equazione:
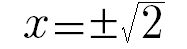
Nonostante sia numeri algebrici che quelli trascendenti siano infiniti, gli ultimi sono infinitamente di più dei primi! Ebbene sì: esistono infiniti più grandi di altri infiniti.
Il famoso pi greco (3.14159…), per esempio, fa parte della famiglia dei numeri trascendenti! Infatti non è possibile scrivere un’equazione con coefficienti interi o razionali che ammetta, tra le proprie soluzioni, il numero pi greco.
Cosa ci è stato richiesto?
Per prima cosa dobbiamo fare amicizia con questi numeri e con i loro sviluppi formali per arrivare ad approssimarli con rapporti polinomiali o altre funzioni.
Ma l’obiettivo veramente interessante e quindi anche più complesso (perché per noi bello è sinonimo di tosto!) è quello di realizzare una libreria di procedure che permetta a chiunque di giocare con i numeri trascendenti: calcolare gli sviluppi con tantissime cifre decimali, verificare somiglianze, immaginare teoremi …
La libreria, realizzata con Blockly si può provare direttamente su questo blog seguendo questo collegamento.
Il senso di Smilla per la neve
C’è un breve brano de Il senso di Smilla per la neve, romanzo di Peter Høeg, in cui la protagonista, Smilla per l’appunto, paragona i numeri a un panorama immenso e infinito da esplorare.
Lo stesso brano è ripreso nel film omonimo ed è proprio quel breve spezzone video che, in un certo senso, ha dato il via a tutto il progetto RiA – research in Action, come racconta l’insegnante che lo ha progettato in questo stesso blog.



