Questo laboratorio è stato sviluppato da Claudio Acciardi, Margherita Bartoli, Daniele Marafini, Dante Mazzaroppi, Denise Salerno in collaborazione con Donato Bini (CNR-IAC), il progetto è stato coordinato da Gualtiero Grassucci (lss G.B. Grassi di Latina).
Il problema consiste nel trovare le condizioni nelle quali un gas di fotoni raggiunge l’equipartizione energetica. Per raggiungere questo obiettivo il gruppo ha utilizzato simulato differenti situazioni di distribuzione dell’energia utilizzando l’indice di Gini come misura della distribuzione dell’energia nel sistema. Dai dati raccolti si evince trovando un rapporto di proporzionalità inversa tra diseguaglianza e temperatura, e tra diseguaglianza e numero di microstati.
Un gas di fotoni è un sistema fisico formato da fotoni che si comportano e hanno caratteristiche analoghe ad un gas tradizionale. Vista la sua natura quantistica però, l’energia di questo sistema è esprimibile solo attraverso pacchetti discreti. Per calcolare l’energia media in uno stato n utilizziamo questa formula:
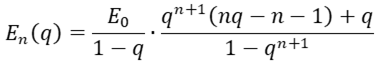
Dove
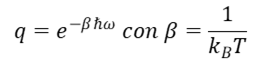
e T è la temperatura del gas e n è il numero dello stato.
Modificando il valore di q e il numero totale di microstati N, è possibile raccogliere dei dati, che poi vengono rappresentati e analizzati (su un piano cartesiano si rappresentano le percentuali dell’energia cumulata rispetto alla percentuale di fotoni che posseggono quell’energia ottenendo la curva che descrive sostanzialmente la distribuzione di un certo stato). L’obiettivo del progetto è trovare la giusta combinazione di valori per i quali questa distribuzione è la più equa possibile, e trovare una correlazione tra iniquità e caratteristiche dello stato.
La soluzione
La simulazione è stata ripetuta più volte variando i valori iniziali e confrontando successivamente i risultati. Man mano che si moltiplicavano le simulazioni diventava sempre più evidente un legame tra il valore di q, il numero di microstati e la distribuzione energetica nello stato: i dati suggeriscono che all’aumentare di N la distribuzione risulta più equa.
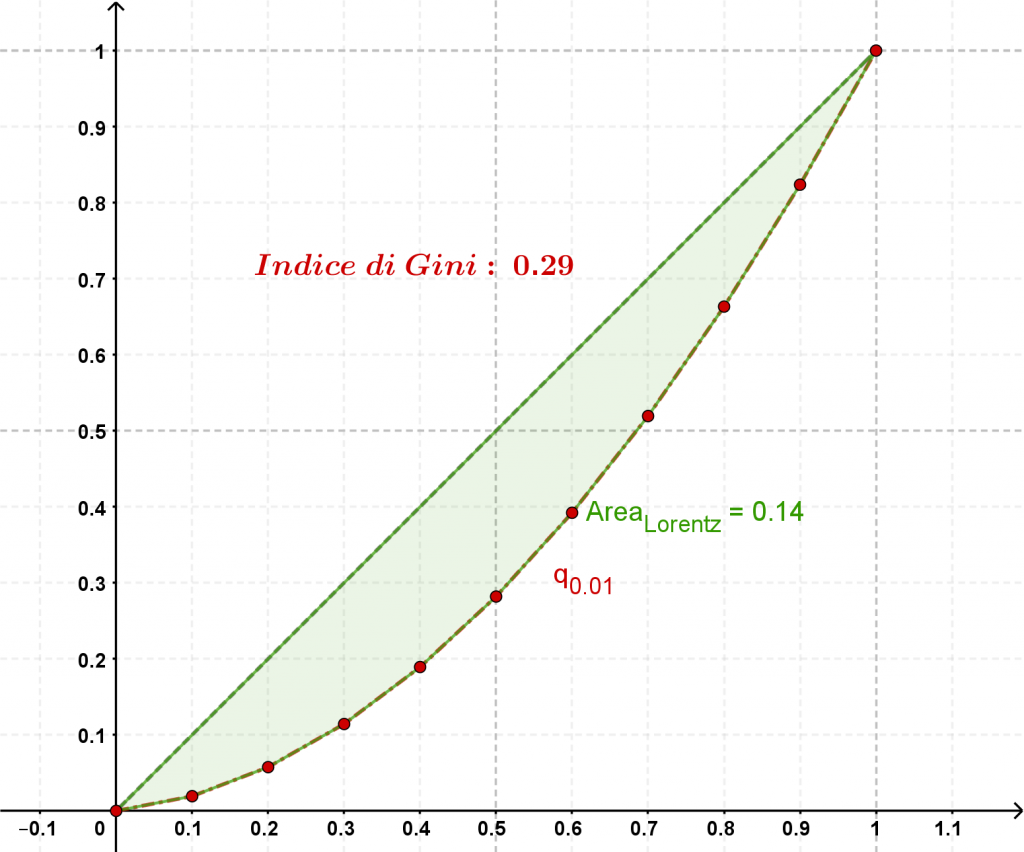
Anche aumentare il valore di q porta generalmente a una riduzione del valore dell’indice di Gini (e quindi a una distribuzione più equa), ma, arrivati ad un certo valore limite, la curva supera la bisettrice. Il valore limite cambia per ogni N.
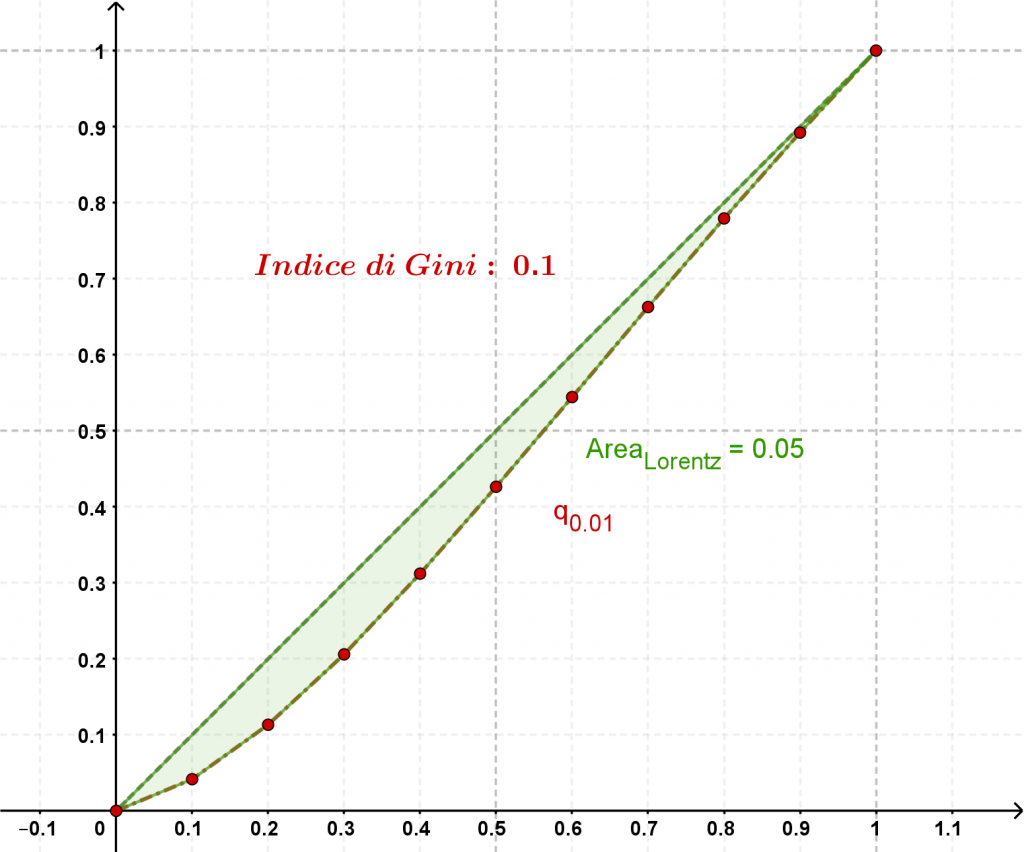
La figura che segue mette in relazione il valore di q e l’indice di Gini calcolato sulla curva prodotta da quel valore, una buona approssimazione della funzione G=G(q) che realizza questa correlazione appare essere
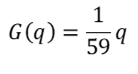
con un errore inferiore a 10-3.
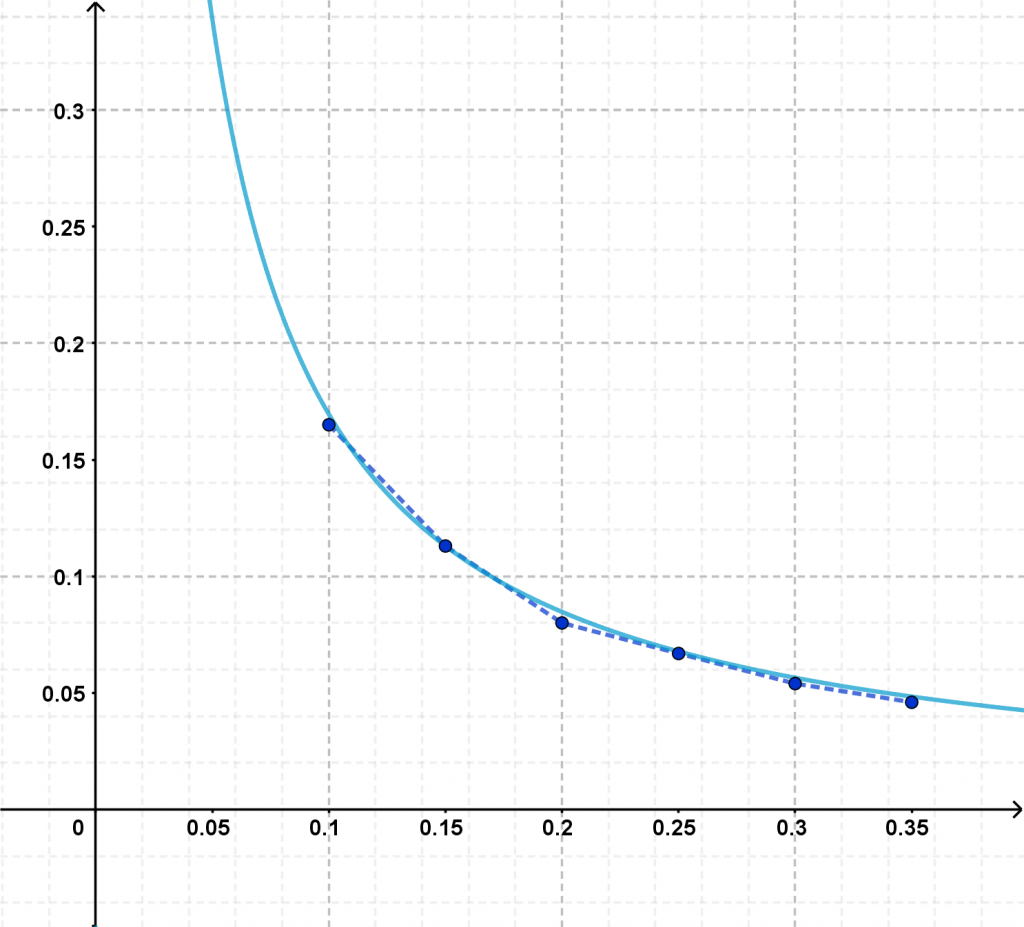
Conclusioni
Nel corso del laboratorio siamo riusciti a comprendere meglio il funzionamento del sistema fisico del gas di fotoni, trovando legami tra i valori dell’energia, espresso dal parametro q, il numero di microstati e la distribuzione dell’energia. Lo stato con la distribuzione più equa dovrà avere un numero di microstati molto alto e un valore di q prossimo al valore limite. Inoltre è stato trovato anche un legame tra q e l’indice di Gini G, espresso dalla funzione approssimante G(q).