L’approssimazione dei numeri trascendenti è affrontata in uno dei laboratori del progetto.
Abbiamo già visto come approssimare il valore di pi greco utilizzando l’elegante formula che deriva dallo sviluppo in serie di Taylor della funzione arcotangente. Questa volta partiamo da un problema proposto da George-Louis Leclerc de Buffon nel 1777 che più o meno si presenta in questo modo: se lasciamo cadere in modo completamente casuale degli aghi su un foglio su cui sono state tracciate delle linee parallele (la cui distanza è di poco superiore alla lunghezza degli aghi), quale sarà la probabilità che un ago tocchi una delle linee?
Il video qui di seguito cerca di spiegare come questo problema sia legato al valore di pi greco …
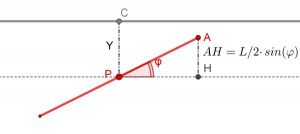
Qui di seguito è schematizzata la situazione nel caso che l’ago tocchi una delle linee tracciate sul foglio. Se Y è la distanza del punto medio dell’ago dalla linea più vicina, l’ago tocca la linea solo se questa distanza Y è minore (o uguale) alla distanza AH.
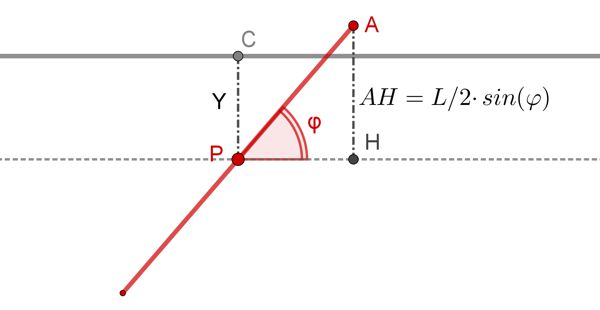
Ora esaminiamo la situazione opposta, in cui l’ago non tocca nessuna delle linee.
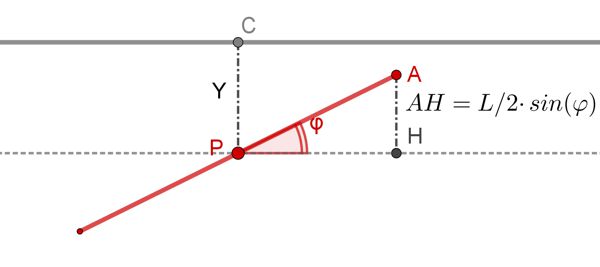
È chiaro che, se la distanza Y del punto medio dell’ago dalla linea più vicina è maggiore della distanza AH allora l’ago non tocca nessuna delle linee. In altre parole, i casi favorevoli (l’ago tocca una delle linee) corrispondono alla condizione:
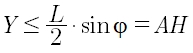
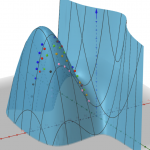
A questo punto è interessante tracciare la curva che rappresenta la lunghezza AH in funzione dell’angolo phi:
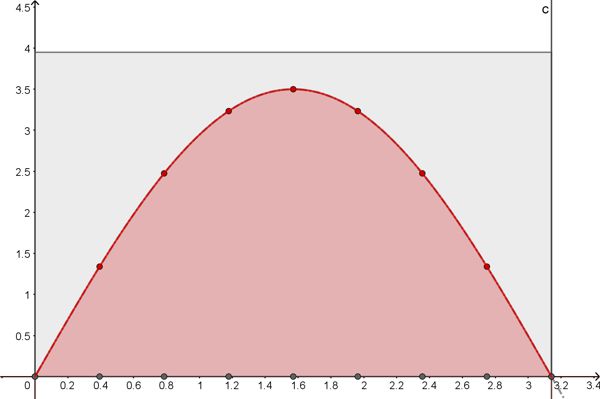
In questa rappresentazione, il rettangolo grigio contiene tutte le possibili posizioni di un ago (compreso ogni possibile orientamento) mentre l’area in colore rosa indica le possibili posizioni dell’ago in cui la distanza Y del punto medio dalla linea più vicina è inferiore alla distanza AH.
Quindi: la probabilità p che l’ago tocchi una delle linee è data dal rapporto tra l’area rosa e la superficie del rettangolo grigio:
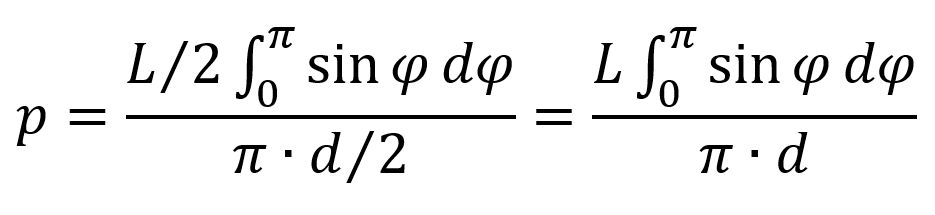
Visto che l’integrale ha come risultato 2, la probabilità cercata è
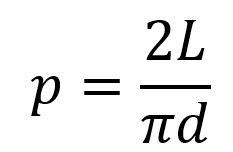
che fornisce, incidentalmente, una formula per pi greco:
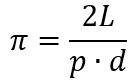
Ora, se determiniamo in modo euristico la probabilità p lanciando casualmente un gran numero di aghi su un foglio a righe, possiamo indirettamente determinare un’approssimazione di pi greco utilizzando proprio l’ultima formula.
Nel nostro caso abbiamo lanciato 3000 aghi di lunghezza L = 7cm, lasciandoli cadere su un foglio sul quale erano state tracciate delle linee parallele a distanza d = 8cm l’una dall’altra. 1671 di questi aghi sono caduti in modo da toccare una riga. Abbiamo quindi stimato la probabilità come il rapporto tra gli aghi che hanno toccato una linea (1671) e il totale degli aghi lasciati cadere (3000). A questo punto abbiamo potuto stimare il valore di pi greco:
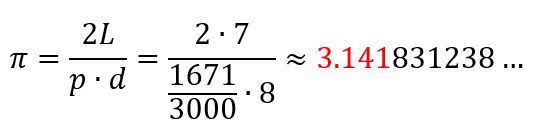
Tre cifre decimali corrette!