Aggiornamenti (2)
Articolo realizzato in collaborazione con Alessio De Cesare, Stefano Manauzzi, Lorenzo Pazienza, Francesco Scaldarella e Lavinia Soldera, autori del laboratorio 18 – Modelli per le epidemie.
I nuovi laboratori affrontati quest’anno (2022-2023) hanno richiesto l’integrazione del Toolbox che ora è alla revisione 3.1 (21.05.23). È stato aggiunto un nuovo capitolo: 7. Equazioni differenziali, che suggerisce un procedimento per costruire la soluzione di un’equazione differenziale senza risolvere l’equazione stessa. Il laboratorio 18 – Modelli per le epidemie utilizza proprio questo metodo per ricavare l’andamento delle funzioni che risolvono le equazioni differenziali dei principali modelli per le epidemie.
In breve
Dato un problema di Cauchy del tipo

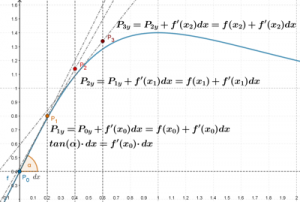
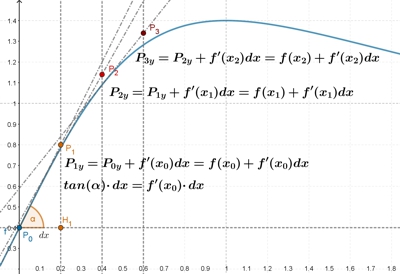
si può cercare approssimare la soluzione costruendo una successione di punti a partire da quello fornito, implicitamente, dalle condizioni del problema di Cauchy P0(x0, y0). Infatti, una volta scelto un incremento dx per la variabile x, si può innanzitutto determinare l’ascissa x1 del punto successivo della successione come x1 = x0 + dx e successivamente stimare l’ordinata y1 dello stesso punto: y1 = y0 + f'(x0)dx.
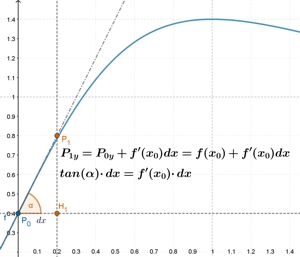
Infatti l’incremento dy della variabile y si può approssimare per mezzo della derivata prima della funzione: dy = f'(x0)dx. In pratica, il cateto H1P1 del triangolo P0P1H1 si determina (usando il secondo teorema sui triangoli rettangoli della trigonometria) come prodotto tra il cateto P0H1 = dx per la tangente dell’angolo opposto al primo cateto. Ma la tangente goniometrica dell’angolo è anche la derivata della funzione nel punto di tangenza.
È vero che non conoscendo la soluzione y = f(x) dell’equazione differenziale non conosciamo nemmeno la sua derivata ma possiamo usare l’equazione differenziale per approssimare la derivata nel punto P0.
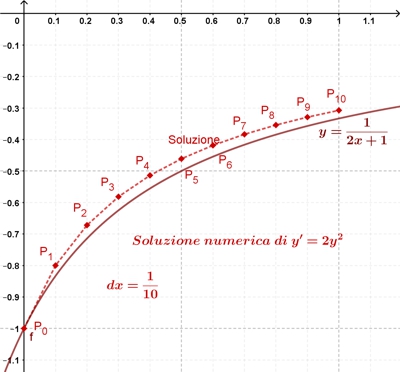
Per esempio, se l’equazione differenziale è y’ = 2y2, con y(0) = -1, il primo punto della successione sarà P0(0, -1). Scegliamo dx = 0.1, abbiamo x1 = x0 + dx = 0 + 0.1 = 0.1 mentre f'(x0) = 2y02 = 2 (-1)2 = 2. Quindi ora possiamo stimare l’ordinata del punto successivo P1: y1 = y0 + f'(x0)dx = -1 + 2 0.1 = -0.8 e quindi P1(0.1, -0.8).
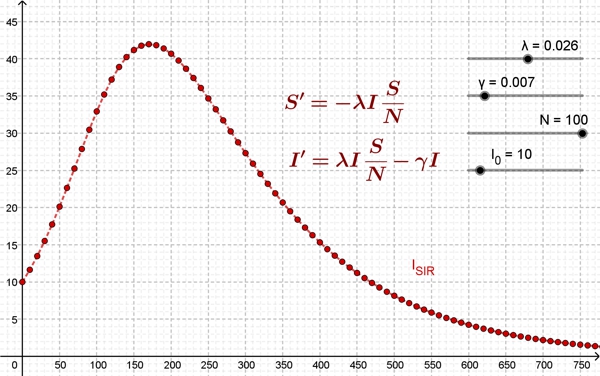
Il modello SIR
Il modello SIR (il cui nome completo è Suscettibili – Infettivi – Rimossi) è regolato dal sistema di equazioni differenziali
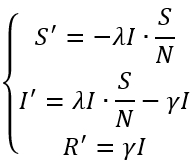
dove lambda è il tasso di contagio e gamma il tasso di guarigione.
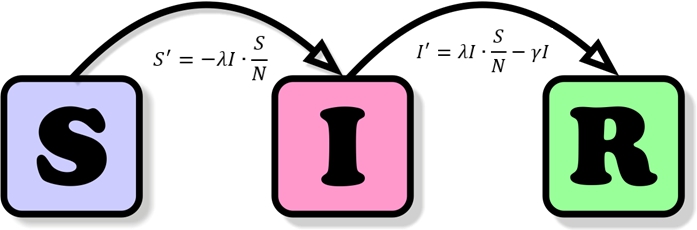
In altre parole, il modello SIR prevede che per ogni unità di tempo il numero di suscettibili (raccolti nell’insieme S) diminuisca di S’ perché contagiati e quindi spostati nell’insieme degli Infettivi I. Nello stesso intervallo di tempo gli Infettivi aumentano di S’ (sono i suscettibili che sono stati infettati) ma contemporaneamente diminuiscono perchè i guariti e i deceduti sono spostati nell’insieme dei Rimossi R.
Non potendo, con le competenze di un quarto superiore, determinare analiticamente le funzioni S(t), che descrive il numero di suscettibili nel tempo, e I(t), gli infettivi giorno per giorno, abbiamo usato il metodo di approssimazione visto sopra per costruire una successione di punti S0, S1, … e un’altra successione I0, I1, … in modo da avere un quadro abbastanza chiaro dell’andamento delle corrispondenti funzioni S(t) e (I(t).
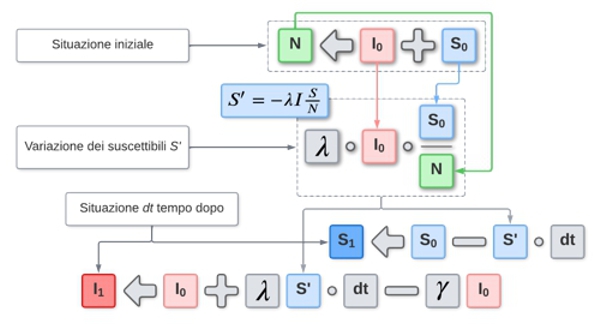
Il metodo usato, come già detto, è spiegato in dettaglio nel Toolbox. Nel materiale a supporto del laboratorio Modelli per le epidemie 2.0, tra gli altri, si trovano due file GeoGebra che implementano, utilizzando il foglio di calcolo dell’applicazione, le soluzioni delle equazioni differenziali del modello SIS e SIR.