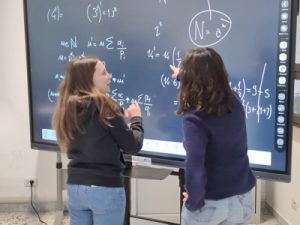A cura di Silvia De Nardis, Andrea Gardella, Chiara Gatto, Martina Torre. Questo articolo espande il laboratorio La derivata aritmetica.

Anti-derivata aritmetica

Per coloro che arrivano dal nostro laboratorio sulla derivata aritmetica: benvenuti! A chi invece non l’ha ancora letto consigliamo di recuperarlo. Il laboratorio sulla derivata aritmetica si può scaricare qui. Questo breve e interessante approfondimento è indipendente dal fascicolo, ma forse potrebbe essere necessario spulciarlo per alcune importanti e curiose nozioni.

L’anti-derivata è per la derivata aritmetica ciò che l’integrale è per la derivata analitica. 

derivata analitica sta a integrale come derivata aritmetica sta ad anti-derivata

Infatti, la notazione per l’antiderivata di n’ è

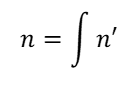
esattamente la stessa degli integrali. Purtroppo, dato un numero n’ qualsiasi, non esiste alcuna formula o metodo generale sempre valido per ricavarne la primitiva, ossia il numero n la cui derivata fa n’. 

Ci sono, però, dei metodi che permettono di calcolare l’anti-derivata di alcuni casi particolari, quando n’ risponde a specifiche caratteristiche. Un indizio si trova nell’ultima tabella del primo capitolo del nostro fascicolo (cfr. La derivata aritmetica – la nuova frontiera della teoria dei numeri? Ancora un po’ di esercizi a pagina …).

Ricordiamo che, dato numero naturale n e la sua scomposizione in numeri primi

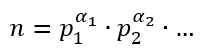
la derivata aritmetica di n è definita come

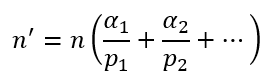
Così, per esempio,

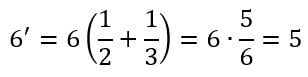
oppure

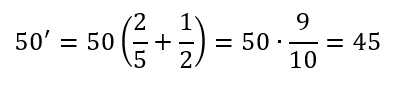
Per quello che ci interessa sono interessanti i numeri naturali 6, 14, 21, 22, 25, … che si possono scomporre in un prodotto di due primi con esponente uno. La derivata di questi numeri, come è facile verificare utilizzando la definizione di derivata aritmetica fornita in precedenza, è sempre la somma dei loro fattori. Potremmo azzardare l’ipotesi che ogni numero che può essere scritto come la somma di due numeri primi, non necessariamente distinti (come per esempio 10 = 3+7 = 5+5), è l’anti-derivata del numero che si ottiene moltiplicando i due addendi. Ma andiamo con calma: sappiamo che tutto deve essere dimostrato e niente lasciato al caso. 

Prendiamo un numero n che può essere scomposto come prodotto di due numeri primi: n=p₁*p₂. Sapreste farne la derivata?

Si vede subito che

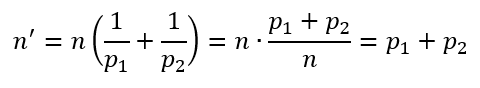
Abbiamo appena dimostrato che, se un numero naturale n si può scrivere come prodotto di due primi, la derivata n’ di n è uguale alla somma dei due fattori della scomposizione.  Grazie a questa peculiarità, che però abbiamo appena dimostrato essere sempre vera, il calcolo dell’anti-derivata può diventare estremamente semplice se si riesce ad esprimere il numero osservato come la somma di 2 numeri primi.

La congettura di Goldbach

Proponiamo una curiosa parentesi ai nostri lettori più intrepidi: non sarà facile ma armatevi di carta e penna così – sotto la nostra fidata guida – riuscirete a trovare un nuovo tassello di quel meraviglioso puzzle che la matematica è.

Forse saprete che gli spunti di riflessione possono provenire dai luoghi più remoti e sorprendenti. Infatti vi dobbiamo portare nell’antica Königsberg, nella Prussia orientale (ora la città si chiama Kaliningrad ed è un’enclave russa tra Polonia e Lituania). Proprio lì, nel lontano 1742, il matematico Christian Goldbach formulò la sua famosa congettura che afferma che:

Ogni numero pari n, maggiore di 2, è esprimibile come somma di due numeri primi, eventualmente identici.

L’idea di Goldbach è stata, negli ultimi tre secoli, collaudata più e più volte e in molti vi si sono cimentati nel tentativo di dimostrarla. Fino ad oggi la congettura è stata testata per valori di n ≤ 16 · 10¹⁷. Sappiamo, però, che verificare una congettura pure se fosse per milioni, miliardi di tentativi, non è sufficiente come dimostrazione. Un vero peccato, perché questa congettura potrebbe essere molto utile per proseguire la nostra ricerca.

Vi viene in mente un collegamento tra la congettura di Goldbach e qualcosa che avete appena studiato? Se non vi viene nulla in mente vi diamo una mano: nel paragrafo precedente era rimasto un interrogativo in sospeso riguardante l’anti-derivata.

Avevamo dovuto constatare, con grande sconforto, che allo stato attuale delle cose non esiste un metodo generale e universale per integrare un numero n e trovare così la sua (o le sue) primitive. Eppure, per alcuni numeri particolari, il lavoro diventava veramente semplice. Stiamo parlando di numeri n’ esprimibili come la somma di due primi non necessariamente distinti (n’ = p₁ + p₂). Messa in questo modo, la correlazione tra la congettura di Goldbach e il nostro problema dovrebbe essere più chiara.

Vi viene in mente almeno una categoria di numeri che, se la congettura fosse dimostrata, potrebbe essere sempre integrata con grande facilità?

Stiamo parlando proprio dei numeri pari! Non si tratta di un teorema, e questo lo sappiamo, però ciò non vuol dire che non possiamo comunque ragionare sulle implicazioni che la congettura potrebbe avere. Infatti, abbiamo appena scoperto che dato un numero n esprimibile come la somma di due primi, la sua anti-derivata non è altro che il prodotto di quegli stessi numeri primi. Se questa congettura fosse dimostrata sarebbe un grande vantaggio nella ricerca delle anti-derivate, come lo sarebbe un metodo per trovare i due numeri primi la cui somma dà la derivata di un numero. Così facendo avremmo trovato tutte le anti-derivate di ogni numero pari (basta trovare tutte le coppie di primi le cui somme danno il numero). E non solo, la stessa regola vale per tutti i numeri come p+2, con p primo!

In realtà si semplificherebbe anche il metodo per ricavare alcune derivate, come scopriremo nel paragrafo successivo… 

Primitive

Questo nuovo metodo, un po’ meno generale ma più veloce nei casi in cui lo si può applicare, ci può aiutare a scoprire una particolarità molto curiosa dell’anti-derivata che forse alcuni di voi avranno già intuito.

Provate a scrivere 10 come somma di due numeri primi e poi trovate i numeri di cui 10 è la primitiva. Per questo esercizio, però, abbiamo un’ulteriore richiesta: se possibile, cercate di svolgerlo contemporaneamente (ma senza consultarvi) ad altre persone. 

Se invece siete da soli, vi dobbiamo chiedere uno sforzo in più: scrivete 10 come tutte le somme di primi che vi vengono in mente. In ogni caso, vi sarete accorti che la primitiva di 10 è 25. O che la primitiva di 10 è 21. O entrambe.

Ecco: stiamo scoprendo che quando si parla di anti-derivata, la questione si inizia a fare complicata. In realtà sia 21 che 25 sono le primitive di 10. Il rapporto tra derivata aritmetica e primitiva infatti non è esclusivo (anche se già lo avevamo accennato) e che il risultato dell’anti-derivata non deve necessariamente essere un numero, ma può corrispondere ad un insieme. Vediamo se riuscite a fare da soli …

Prendiamo in esame il numero intero n = 100. Trovate il modo di scrivere cento come somma di due numeri primi.

Per esempio, se pensiamo 100 = 47 + 53 allora 47 x 53 = 2491. Ci sono cinque possibilità di scomporre 100 come somma di due numeri primi, quindi ci sono cinque possibili antiderivate di 100:

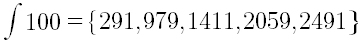
Osservate quello che avete ottenuto. C’è qualche regolarità nelle coppie di primi? C’è un modo di trovare una formula che permetta di scomporre un numero intero nella somma di due numeri primi?

Non è facile trovare una risposta, magari proviamo con un secondo numero.

Ripetete il procedimento per n = 80. Ci sono regolarità, proprietà, che consentono di automatizzare la procedura?

Se siete in difficoltà o non avete avuto idee non vi preoccupate. Non solo non c’è una formula per determinare la primitiva di un numero, ma non esiste nemmeno un metodo per determinare quante risposte aspettarsi. Ma c’è un numero speciale con una miriade, anzi, addirittura infinite primitive.

È 1! Attenzione: si tratta di un’esclamazione, non è 1! (il fattoriale di uno) anche se 1! = 1).

Purtroppo allo stato attuale non esiste un modo universale e sempre valido per trovare l’anti-derivata di un numero (questo non significa necessariamente che esso non possa essere trovato) ma se così fosse, integrando 1 otterremo tutti gli infiniti numeri primi esistenti facendo crollare molti dei moderni sistemi di crittografia.

Immaginate di poter mettere in ginocchio i sistemi bancari semplicemente trovando l’antiderivata di uno.

Questi nuovi sentieri matematici che stiamo scoprendo dovrebbero farvi capire che forse la derivata aritmetica è meno inutile di quanto non potesse sembrare. Ma al di là delle applicazioni pratiche, immaginate quali altri potrebbero essere gli sbocchi non ancora individuati, non solo della derivata aritmetica ma di tutte le nuove frontiere matematiche. Certo, alcune strade si potranno rivelare vicoli ciechi, strade senza uscita, ma è impossibile saperlo senza prima averle esplorate.

I moderni sistemi di protezione dei dati, in particolare l’algoritmo RSA che è tra i più utilizzati, utilizzano un metodo a chiave pubblica: il messaggio cifrato è inviato al destinatario insieme alla chiave che è il prodotto di due numeri primi molto grandi. Il destinatario è in grado di determinare rapidamente i due numeri primi e con quelli decifrare il messaggio. La sicurezza del sistema si basa sul fatto che la scomposizione di un prodotto di due primi nei suoi fattori è un’operazione estremamente dispendiosa proprio perché non è facile trovare i numeri primi da provare.

Il matematico Riemann ha ipotizzato un metodo per trovare gli infiniti numeri primi senza ricorrere alla scomposizione in fattori primi. Questa ipotesi non è stata dimostrata e quindi rimane ancora oggi una congettura. La sua dimostrazione sarebbe una scoperta matematica dagli incredibili risvolti nei più svariati ambiti. Se vi ha incuriosito vi suggeriamo una breve ricerca autonoma.