La nuova frontiera dei numeri?
Questo laboratorio è stato sviluppato da Silvia De Nardis, Andrea Gardella, Chiara Gatto, Martina Torre in collaborazione con il prof. Donato Bini (Istituto per le applicazioni del calcolo Mauro Picone di Roma). Vedere anche Anti-derivata aritmetica.
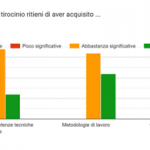
Il parere del tutor esterno
… Sono semplicemente sbalordito dalla mole di lavoro che i ragazzi hanno fatto e dal modo con cui i risultati sono stati ri-organizzati nei fascicoli. La mia non può che essere una valutazione estremamente positiva (ti prego di estenderla ai ragazzi!) e continuo a pensare che sono molto fortunati a poter vivere questa esperienza. Non ho nulla da aggiungere ai fascicoli.
Dunque …congratulazioni agli studenti …e al loro Prof!!!!
prof. Donato Bini (CNR-IAC)
Se in un test venisse richiesto di derivare 5, 44.324.115, radice di due o pi greco, i nostri lettori più ferrati nel calcolo differenziale, senza farsi prendere dal panico, risponderebbero con tranquillità … zero! Del resto, tutti noi sappiamo che la derivata di una costante additiva è sempre nulla.
O forse no? Preparatevi a mettere in discussione le vostre certezze poiché coloro che sono stati presi dal panico ne avevano ben donde: vi porteremo nel mondo della derivata aritmetica dove l’unica regola rassicurante del calcolo differenziale perde di valore e derivare un numero diventa un processo tanto insidioso quanto entusiasmante.
Con questo laboratorio intendiamo fornire una breve introduzione ad una branca nuova e non del tutto esplorata della teoria dei numeri: quella che si occupa della derivata aritmetica. Si tratta di un’operazione che, nonostante la denominazione simile, ha poco a che vedere con la derivata analitica che siamo soliti trovare nei libri di testo. Con la derivata aritmetica deriviamo un numero (non una funzione) ottenendo come risultato un altro numero (non il tasso di variazione istantaneo della funzione in un dato punto).
Per questo laboratorio è disponibile il fascicolo 21 – Derivata aritmetica e alcuni articoli e proposte di ampliamento su questo sito. Con l’occasione è stata rivista la libreria per l’approssimazione dei numeri trascendenti e per, ovviamente, calcolare la derivata aritmetica.
Prerequisiti
Per questo laboratorio è necessario:
- Conoscere la scomposizione in fattori primi.
- Conoscere e comprendere il concetto di sommatoria e produttoria.
- Conoscere il concetto di derivata analitica e relative formule.
- Comprendere il significato (in termini generali) di integrale.
Obiettivi
Gli obiettivi principali sono:
- Definire il concetto di derivata aritmetica.
- Imparare a dimostrare semplici formule a partire da una definizione.
- Familiarizzare con la derivata (aritmetica) di numeri interi e scoprirne le caratteristiche attraverso una serie di esercizi.
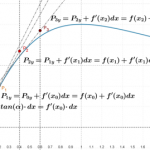
- Legare il concetto di derivata aritmetica alla sua interpretazione geometrica.
- Definire la derivata aritmetica di una frazione.
La derivata aritmetica
La derivata aritmetica è una funzione che associa (inizialmente) a ogni intero non negativo un numero anch’esso intero basato sulla sua scomposizione in fattori primi. Più precisamente, se n è un numero intero che si può scomporre in un prodotto di primi come segue: n = (p1)a1 (p2)a2 … (pt)at allora la sua derivata aritmetica è
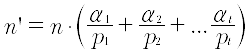
L’idea di base fu proposta nel 1911 al Congresso nazionale della Sociedad Matemática Española da José Mingot Shelly e rappresenta un argomento che ha occupato poche risorse della società matematica internazionale. Si tratta di un’operatore che, nonostante la denominazione simile, ha poco a che vedere con la derivata analitica che siamo soliti trovare nei libri di testo. Con la derivata aritmetica si deriva un numero (non una funzione) ottenendo come risultato un altro numero (non il tasso di variazione istantaneo della funzione in un dato punto). Eppure presenta alcune curiose caratteristiche e proprietà (ma non ne possiede altrettante, se non di più, proprietà della derivata analitica).
Con questo laboratorio intendiamo fornire una breve introduzione ad una branca nuova e non del tutto esplorata della teoria dei numeri proponendo, come è nostro solito, un’indagine matematica alla scoperta delle proprietà e delle caratteristiche della derivata aritmetica.