Un gioco da tavolo ambientato a Königsberg
Il problema dei sette ponti di Königsberg non cessa di affascinare matematici e non matematici! È da poco stato pubblicato dalla Puzzling Pixel Games un gioco da tavolo: Seven Bridges, opera di Ronald Halliday, grafico e autore di giochi. Un’eccellente recensione del gioco si può trovare sul sito della Tana dei Goblin. Il regolamento del gioco è disponibile online sul sito della Puzzling Pixel Games.
Un perfetto complemento al laboratorio Quattro passi in centro!
Il dilemma
Il problema che porta il nome della città, e che fornì l’occasione a Leonhard Euelr per inventare la teoria dei grafi e la topologia, si può enunciare con poche parole:
è possibile immaginare un percorso in città in modo da attraversare tutti i sette ponti sul fiume Pregel, passando su ognuno di essi una e una sola volta?
La soluzione è dovuta a Euler: è impossibile! La spiegazione è ormai nota come Teorema di Euler ed è il primo teorema della storia relativo alla teoria dei grafi. Su questo sito potete trovare un buon laboratorio che vi farà riscoprire il teorema: Quattro passi in centro. Gli altri laboratori disponibili per lo stesso argomento si possono trovare nella pagina Topologia e teoria dei grafi.
Il gioco
In breve. A ogni turno il primo giocatore lancia sei dadi speciali che riportano sulle facce vari tipi di strade e incroci, ogni giocatore, a partire dal primo, sceglie uno dei sei dadi e traccia sulla mappa (riportata sulla propria plancia) i tratti di strada indicati dal dado agganciandoli al percorso già esistente.
Alcune semplici regole governano il modo in cui è possibile costruire il percorso. Per esempio, a eccezione dei primi due mostrati qui di seguito, ogni altro tratto deve essere tracciato completamente all’interno di una sola casella in cui è divisa la mappa.

La partita dura in tutto cinque turni e, indipendentemente dal numero di partecipanti, ogni giocatore avrà a disposizione 30 dadi per costruire il percorso migliore, quello che porterà il maggior numero di punti. Si fanno punti, infatti:
- per il percorso chiuso con il maggior numero di angoli,
- per i ponti attraversati (ovviamente),
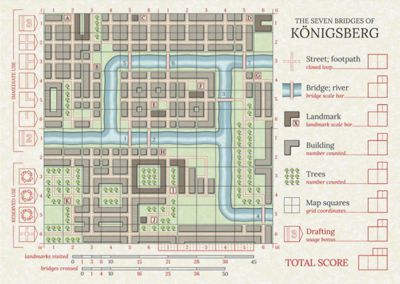
- per i luoghi caratteristici visitati (ce ne sono undici sulla mappa, indicati da lettere maiuscole),
- per il numero di edifici …
- … o di alberi che si affacciano sul nostro percorso,
- per le strade che portano fuori dal centro città,
- per i bonus utilizzati (che sono riportati sulla sinistra della plancia del giocatore).
Caratteristica divertente: ci sono sette modi per fare punti ma, alla fine della partita, ogni giocatore ne potrà usare solo in numero pari ai ponti attraversati dal percorso costruito, rinunciando a quelli con il punteggio inferiore (p.es.: se il suo percorso attraversa solo quattro ponti, al termine della partita potrà contare solo i quattro punteggi migliori tra quelli elencati sopra). Un simpatico richiamo ai sette ponti dell’enigma!
Un esempio
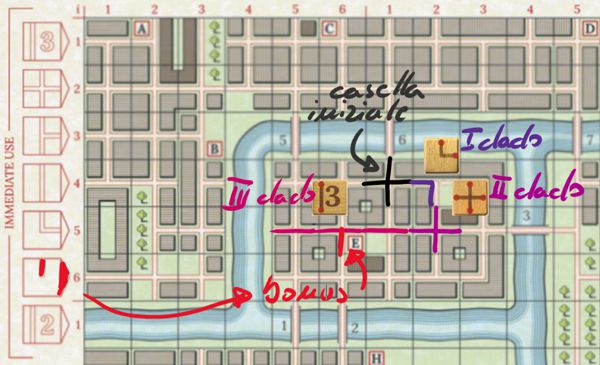
Qui di seguito un breve esempio di gioco. Si tratta di una partita a due giocatori (e quindi, ogni giocatore sceglie tre dadi a turno) ma qui è mostrata solo la plancia di uno dei due. A inizio partita i giocatori si accordano su una casella di partenza, la stessa per entrambi. Qui è stata scelta la casella che si trova nella riga 4 e colonna 6 del primo quadrante, quello in alto a destra nella mappa, le strade della casella iniziale sono immediatamente tracciate (in colore nero nella figura che segue): il percorso in città partirà da qui!