Un esempio concreto
Vedi anche Programmare senza un linguaggio di programmazione 1/3. Introduzione a Blockly inoltre propone una serie di videotutorial introduttivi a questo generatore di codice.
Per spiegare meglio la nostra idea di coding la applicheremo a un problema concreto. Quello che segue è la cronaca (in sintesi) di una esperienza di laboratorio proposta al gruppo che si è occupato del Modello affine per la distribuzione della ricchezza. Quando abbiamo affrontato il laboratorio studenti e studentesse avevano già approfittato del corso introduttivo a Blockly presente su questo sito.
Vogliamo costruire un’app che replichi il modello del mercatino di Anirban Chakraborty. Il modello funziona in questo modo: un gruppo di individui, spesso chiamati agenti, hanno una ricchezza iniziale che supporremo uguale per tutti. Coppie di agenti, selezionati a caso, svolgono semplici transazioni finanziarie che prevedono lo spostamento di una certa quantità di ricchezza (una frazione della ricchezza posseduta dal più povero dei due) a vantaggio di un agente scelto casualmente. Lo scopo è studiare la distribuzione della ricchezza che si ottiene dopo un gran numero di transazioni.
Una prima stesura
Dopo un’ampia discussione sul modello e la simulazione con alcuni semplici esempi la bozza l’algoritmo è stato formalizzato in questo modo:
ripeti n volte
scegli due agenti
scegli una frazione della ricchezza del più povero
scegli a caso un agente
aumenta la ricchezza dell’agente scelto
diminuisci la ricchezza dell’altro agenteSe facciamo riferimento alla definizione di algoritmo che abbiamo presentato nel primo articolo appare evidente che siamo ben lontani dall’obiettivo. In particolare:
- non è definito chiaramente un input del programma;
- non è chiaro quanto vale la ricchezza degli agenti;
- ma soprattutto nessuna delle istruzioni è chiara ed elementare.
Input
Concentrando l’attenzione soprattutto sul primo punto critico (l’input) abbiamo realizzato una nuova stesura dell’algoritmo:
transazioni = numero di transazioni
numeroAgenti = numero degli agenti
ricchezzaTotale = la ricchezza di tutti gli agenti
ricchezzaAgenti = ricchezzaTotale / numeroAgenti
ripeti n volte
scegli due agenti
scegli una frazione della ricchezza del più povero
scegli a caso un agente
aumenta la ricchezza dell’agente scelto
diminuisci la ricchezza dell’altro agenteLe modifiche più importanti riguardano proprio i valori, i parametri iniziali del modello (e quindi dell’algoritmo). Ora è chiaro (e leggibile, grazie a una scelta oculata dei nomi delle variabili) quante saranno le transazioni da eseguire, quanti gli agenti e la ricchezza posseduta da ciascuno di loro (anche se non è evidente come memorizzare la ricchezza di ciascuno quando sarà modificata dalle transazioni). Molto meno chiara invece è la procedura per scegliere i due agenti e le procedure per aumentare e diminuire la ricchezza di ciascun agente coinvolto sono molto ambigue.
Scelta dei due agenti
La scelta dei due agenti è una procedura abbastanza complessa anche perché il secondo non può essere uguale al primo. Proviamo a incapsulare in una funzione a parte questo processo. Procediamo in questo modo: scegliamo il primo agente e solo successivamente il secondo in modo che sia differente dal primo (le tre righe in grassetto sono commenti che hanno lo scopo di rendere più chiaro l’obiettivo della mini-procedura).
ScegliAgente(n, p)
restituisce un agente scelto a caso diverso da p
n è il numero degli agenti, p l’agente già scelto
zero se si sta scegliendo il primo
u = p
ripeti finché u = p
u = numero casuale tra 1 e n
restituisci uQuesta porzione di codice si può tradurre in Blockly e testare immediatamente.

La procedura si può mettere alla prova con un piccolo programma di soli sei blocchi.
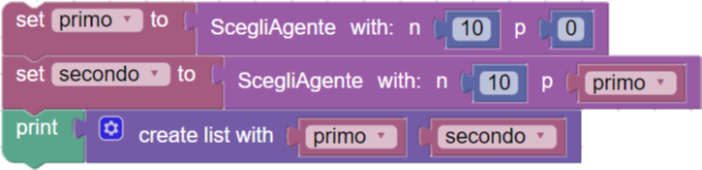
Quando si iniziano a creare funzioni e procedure con Blockly può essere utile leggere Blockly: istruzioni per l’uso 1 su questo stesso sito, ci sono alcune cose da sapere su come il generatore di codice di Google tratta le variabili.
Una seconda stesura
A questo punto siamo pronti per una seconda versione del nostro programma (in grassetto sono evidenziate le due righe in cui usiamo la procedura ScegliAgente). Contemporaneamente abbiamo modificato la fase di inizializzazione supponendo di memorizzare la ricchezza di ogni agente in una lista (la quarta riga della procedura qui di seguito).
transazioni = numero di transazioni
numeroAgenti = numero degli agenti
ricchezzaTotale = la ricchezza di tutti gli agenti
ricchezzaAgenti = crea una lista con tutti gli elementi pari a ricchezzaAgenti:
ricchezzaTotale / numeroAgenti
ripeti transazioni volte
v = ScegliAgente(numeroAgenti, 0)
w = ScegliAgente(numeroAgenti, v)
delta = frazione di minimo(tra ricchezza di v e w)
Scegli a caso un agente
Aumenta la ricchezza dell’agente
Diminuisci la ricchezza dell’altro agenteLa lista della ricchezza degli agenti
La frase:
crea una lista con tutti gli elementi pari a ricchezzaAgenti:
ricchezzaTotale / numeroAgentirichiede tutta una serie di operazioni e quindi potrebbe essere utile racchiudere queste operazioni in una nuova mini-procedura che si occupa solo di inizializzare la lista (le righe in grassetto sono commenti e non codice da eseguire).
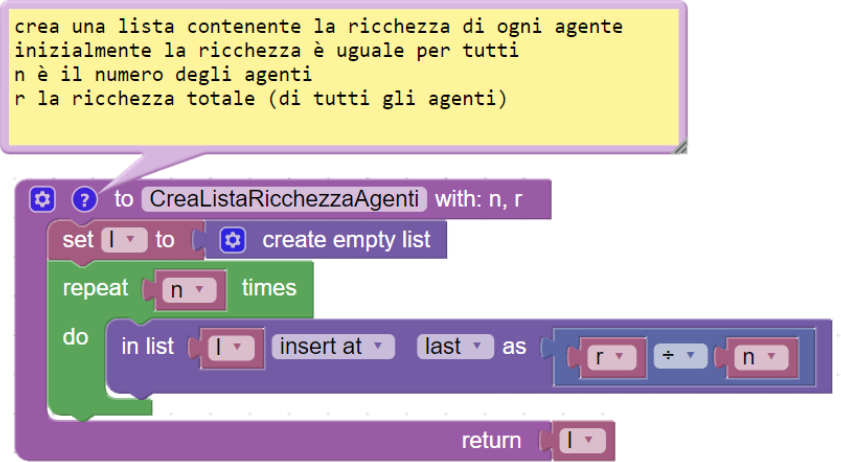
CreaListaRicchezzaAgenti(n, r)
crea una lista contenente la ricchezza di ogni agente
inizialmente la ricchezza è uguale per tutti
n è il numero degli agenti
r la ricchezza totale (di tutti gli agenti)
l = crea una lista vuota
ripeti n volte
in l aggiungi un elemento: r / n
restituisci lQuesta funzione crea la lista l che ha un elemento per ogni agente e la riempie con il valore medio della ricchezza.
Come già visto, anche questa funzione può essere immediatamente messa alla prova con un semplice programma di due soli blocchi:

La seconda stesura ora è decisamente migliore (in grassetto è evidenziata la riga che richiama la funzione appena realizzata).
transazioni = numero di transazioni
numeroAgenti = numero degli agenti
ricchezzaTotale = la ricchezza di tutti gli agenti
ricchezzaAgenti = CreaListaRicchezzaAgenti(numeroAgenti,ricchezzaTotale)
ripeti transazioni volte
v = ScegliAgente(numeroAgenti, 0)
w = ScegliAgente(numeroAgenti, v)
delta = frazione casuale di minimo(tra ricchezza di v e w)
Scegli a caso un agente
Aumenta la ricchezza dell’agente
Diminuisci la ricchezza dell’altro agenteUna terza stesura
A questo punto dobbiamo precisare meglio le frasi Aumenta la ricchezza dell’agente e DIminuisci la ricchezza dell’agente perché i valori corrispondenti devono essere prelevati dalla lista e reinseriti nella lista per l’aggiornamento. Dopo un po’ di lavoro, non facile a dire la verità, si arriva a una versione migliore. L’agente che ottiene vantaggio dalla transazione è scelto calcolando un numero casuale tra 0 e 1 e confrontandolo con il valore medio 0.5 (le righe corrispondenti sono evidenziate in grassetto).
ripeti transazioni volte
v = ScegliAgente(numeroAgenti, 0)
w = ScegliAgente(numeroAgenti, v)
rv = ricchezzaAgenti[v]
rw = ricchezzaAgenti[w]
delta = frazione casuale * minimo(rv, rw)
if numero casuale tra zero e 1 < 0.5
rv = rv + dw
rw = rw – dw
else
v = v - dw
w = w + dw
ricchezzaAgenti[v] = rv
ricchezzaAgenti[w] = rwStesura finale
Possiamo ora concludere racchiudendo il modello del mercatino in un’unica funzione che accetta come parametri i valori iniziali della simulazione (numero degli agenti, ricchezza totale e numero delle transazioni) e restituisce la lista della ricchezza dei singoli agenti dopo aver eseguito le transazioni richieste. In questo caso il programma principale diventa più leggero e leggibile (in grassetto la riga della procedura che richiama la funzione ModelloMercatino.
transazioni = numero di transazioni
numeroAgenti = numero degli agenti
ricchezzaTotale = la ricchezza di tutti gli agenti
visualizza ModelloMercatino(numeroAgenti, ricchezzaTotale, transazioni)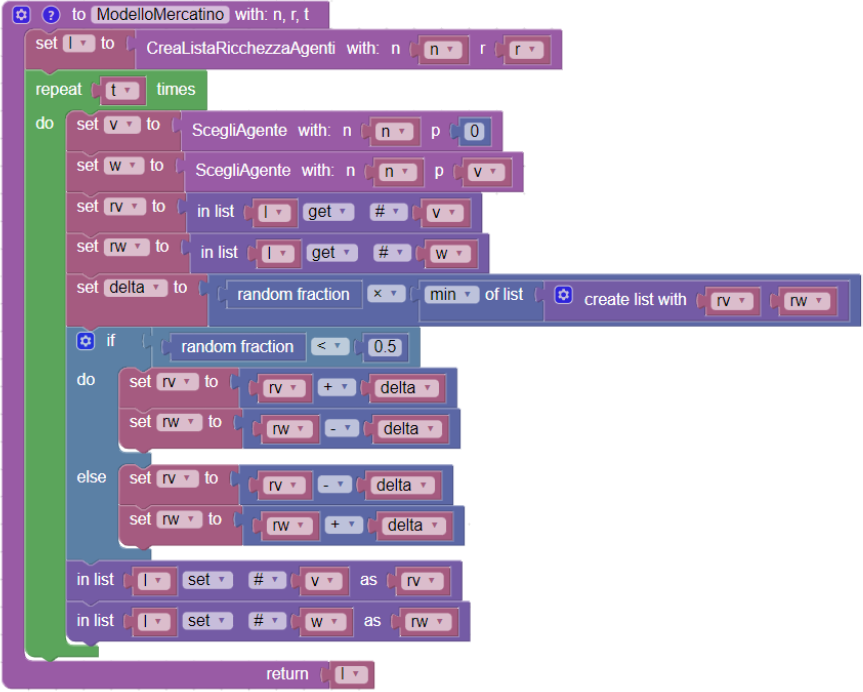
Per concludere, un paio di esempio di come è possibile utilizzare il codice generato da Blockly in altri ambienti.



