Il desiderio di svelare segreti è profondamente radicato nella natura umana; la promessa di partecipare a conoscenze negate ad altri eccita anche la mente meno curiosa. Qualcuno ha la fortuna di trovare un lavoro che consiste nella soluzione di misteri, ma la maggior parte di noi è spinta a soddisfare questo desiderio risolvendo enigmi artificiali ideati per il nostro divertimento. I romanzi polizieschi o i cruciverba sono rivolti alla maggioranza; la soluzione di codici segreti può essere l’occupazione di pochi.
John Chadwick, Lineare B: l’enigma della scrittura micenea.
Quello che avete appena letto è l’incipit di un laboratorio progettato per il primo anno del liceo matematico della nostra scuola, il liceo G.B. Grassi di Latina, seguendo le linee guida degli altri laboratori del progetto.
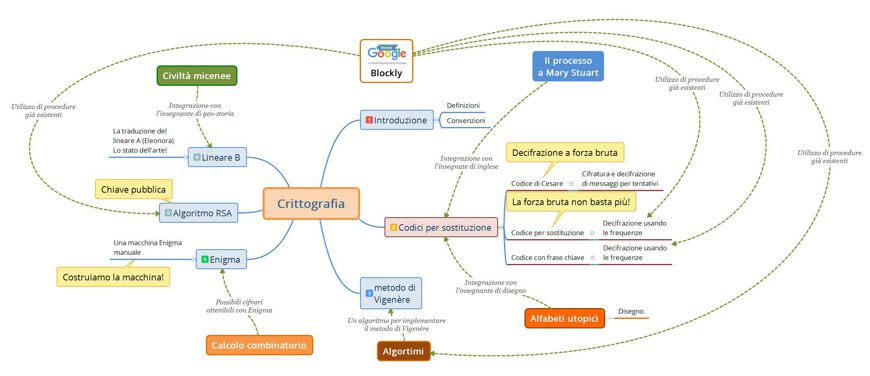
Si tratta di un percorso laboratoriale attraverso i secoli soffermandosi su alcuni dei metodi e degli algoritmi più famosi ideati dall’uomo per nascondere e proteggere messaggi, conversazioni, corrispondenza. Contemporaneamente si cerca di dare un assaggio delle tecniche di criptoanalisi in uso fino all’avvento della crittografia meccanica e automatica.
Il viaggio termina con un excursus nella interpretazione delle lingue morte e, in particolare, con il racconto della traduzione del Lineare B, lingua pre-ellenica (di cui si occupò anche John Chadwick, autore della citazione con cui abbiamo iniziato questo articolo).
Materiale didattico
Gran parte delle attività proposte nel laboratorio sono sviluppate in due fascicoli, nello stile del progetto RiA (vedere la descrizione del laboratorio):
- Crittografia 1 si occupa dei metodi di cifratura diciamo così, manuale, dal codice di Cesare al metodo di Vigenère.
- Crittografia 2 propone attività legate a metodi automatizzati, come la macchina Enigma e l’algoritmo RSA.
Insieme ai due fascicoli/laboratorio, proponiamo un simulatore di Enigma da costruire con carta, forbici e colla perfettamente funzionate, secondo lo schema della famigerata macchina per cifrare tedesca.
Infine, c’è una libreria di procedure e funzioni realizzate con Blockly (come di consueto) che possono essere usate, aggiungendo pochi blocchi, per cifrare e decifrare testi e messaggi usando i metodi affrontati nel laboratorio. La libreria è descritta nel dettaglio, insieme al resto delle attività, qui.
Materiale disponibile su richiesta
Per questo materiale scrivere all’autore o a ria@liceograssilatina.org.
Cifratura con frase chiave – un esempio di criptoanalisi, un esempio descritto passo passo (è una presentazione sia in formato PowerPoint che PDF) di analisi delle frequenze applicata a un testo cifrato con il metodo della frase chiave.
La traduzione del lineare B, la storia della traduzione del Lineare B, una lingua pre-ellenica o minoica, ponendo l’accento in modo particolare sul lavoro di Evans e Chadwick (che richiama le tecniche di criptoanalisi viste in precedenza). Una presentazione per chiudere il laboratorio che racconta la storia dei progressi nella traduzione di questa lingua minoica (per leggere correttamente la presentazione in formato PowerPoint è necessario installare il font aegean.ttf: https://www.wfonts.com/font/aegean.
Schema di una serie di laboratori
- Prerequisiti (i concetti relativi a questi prerequisiti possono essere affrontati in orario curricolare, prima del laboratorio, nel corso dell’anno, oppure forniti e discussi ad hoc nel corso del laboratorio):
- Calcolo combinatorio (fattoriale di un numero, cenni sul binomio di Newton, disposizioni, combinazioni e permutazioni semplici) [1]
- Aritmetica modulare [2]
- Statistica (cenni sulle percentuali e sull’uso delle tabelle)[3]
- Introduzione alla crittografia
- Definizioni (testo e alfabeto in chiaro e cifrato, chiave, convenzioni) Crittografia 1
- Codici per sostituzione Crittografia 1
- Codice di Cesare: si può decifrare con la forza bruta Crittografia 1
- Codice per sostituzione: la forza bruta non basta più, decifrare usando la frequenza delle lettere. Criptoanalisi: forzare un testo usando l’analisi delle frequenze – qui si possono usare le slide della presentazione Cifratura con frase chiave – un esempio di criptoanalisi.
- Costruiamo piccole applicazioni con Blockly [4] (usando procedure e funzioni già presenti) per contare le lettere di un testo.
- Integrazione con matematica: quante sono le possibilità (cenni di calcolo combinatorio).
- Alfabeti utopici (cenni storici sugli alfabeti usati da Mary Stuart, Chaucher, Leon Battista Alberti). Integrazione con disegno. Integrazione con inglese?
- Cifratura con frase chiave Crittografia 1
- Cifratura e decifratura
- Costruiamo piccole applicazioni con Blockly (usando procedure e funzioni già presenti) per cifrare e decifrare rapidamente e per controllare la cifratura eseguita manualmente.
- Criptoanalisi: forzare un testo usando l’analisi delle frequenze, ricostruzione della frase chiave. Blockly. Se non fatto in precedenza, qui si possono usare le slide della presentazione Cifratura con frase chiave – un esempio di criptoanalisi.
- Cifratura e decifratura
- Il problema delle chiavi di cifratura Crittografia 2
- Enigma: meccanizzazione di cifratura e decifratura, schema della macchina, simulatore Enigma (Singh, S. – Codici & segreti, La storia affascinate dei messaggi cifrati dall’antico Egitto a internet, cap. 4 Far breccia in Enigma, pag 162 – 2014, RCS Media Group)
- Integrazione con matematica: calcolo delle possibili configurazioni (della macchina e del simulatore mini).
- Crib: provare a ricostruire la configurazione del simulatore mini conoscendo l’inizio del testo in chiaro, è fattibile? Migliora la situazione se si usa Blockly?
- Algoritmo RSA: come funzione, un esempio semplificato
- Integrazione con matematica: aritmetica modulare
- Enigma: meccanizzazione di cifratura e decifratura, schema della macchina, simulatore Enigma (Singh, S. – Codici & segreti, La storia affascinate dei messaggi cifrati dall’antico Egitto a internet, cap. 4 Far breccia in Enigma, pag 162 – 2014, RCS Media Group)
- La traduzione del lineare B (Singh, S. – Codici & segreti, La storia affascinate dei messaggi cifrati dall’antico Egitto a internet, Il mistero del lineare B, pag 242 – 2014, RCS Media Group) – qui si possono usare le slide della presentazione La traduzione del lineare B.
- Civiltà micenee, il palazzo di Cnosso, la scoperta delle tavolette. Integrazione con geo-storia (eventualmente in compresenza)
- Come è stato tradotto il lineare B
- Come si lavora oggi alla traduzione del lineare A: cenni di machine learning (intervento di un esperto esterno)
[1] Il calcolo combinatorio è usato soprattutto nel paragrafo 2.2 Qualche conticino di Crittografia 2 e 2.4 Forzare Enigma dello stesso fascicolo. Volendo è possibile evitare di usarlo saltando questi due paragrafi, non si pregiudica la comprensione del funzionamento della macchina Enigma (anche se non risulta evidente la complessità delle operazioni di decifrazione).
[2] L’aritmetica modulare è usata sin da subito (paragrafo 2.2 Precisazioni del fascicolo Crittografia 1, nello stesso paragrafo ci sono alcuni cenni sull’operatore modulo), è essenziale per la piena comprensione delle procedure.
[3] L’uso delle percentuali è usato nella criptoanalisi di un testo cifrato (paragrafo 3.2 La criptoanalisi del fascicolo Crittografia 1), sono sufficienti alcuni cenni e la capacità di calcolare una percentuale e di comprenderne il significato
[4] L’idea alla base dell’uso di Blockly è quella di introdurre, per piccoli passi, il coding nel percorso. In questa fase si chiede di montare pochi blocchi (da due a sei) che permettano di richiamare le funzioni già presenti, sviluppate appositamente e disponibili su Research in Action.