Su suggerimento della professoressa Annalisa Malusa (Dipartimento di matematica, Università La Sapienza di Roma) e unitamente alla professoressa Lucilla Galterio (Liceo scientifico G.B. Grassi di Latina) abbiamo sviluppato un percorso per introdurre il calcolo differenziale nelle classi terze del liceo utilizzando l’analisi non standard.
L’analisi non standard è stata formalizzata da Abraham Robinson nel 1966 (Robinson, A. – Non standard analysis – 1996, Priceton Univerity Press), essa recupera alcuni concetti e scelte dell’analisi proposta da Leibnitz e sul finire degli anni novanta è stata oggetto di un esperimento didattico condotta da Giorgio Goldoni (Goldoni, G. – Il calcolo delle differenze e il calcolo differenziale – 2014, Amazon fulfillment).
Il percorso proposto si basa sull’introduzione di un insieme numerico, gli iperreali, che estende i reali aggiungendo infiniti e infinitesimi. Una volta definite le operazioni su questo insieme, estensione delle corrispondenti operazioni sui reali, è possibile manipolare infiniti e infinitesimi senza introdurre il concetto di limite e successivamente definire differenziali e derivate avvicinando il calcolo differenziale agli strumenti algebrici in possesso di studenti e studentesse di una classe terza del liceo scientifico.
Materiale disponibile
Disponibili le slide realizzate per il percorso/laboratorio proposto a una classe terza del liceo matematico nell’anno scolastico 2021/2022:
- 01 – Insiemi numerici: un’introduzione alla definizione degli insiemi numerici che prende spunto da Valenti, S. Dall’intero all’iperreale, un’introduzione graduata all’analisi non standard 1994, GRIM Quaderni di ricerca didattica n.5 con particolare attenzione alle proprietà delle operazioni fondamentali
- 02 – Iperreali: propone le soluzioni di alcuni problemi di geometria analitica (suggeriti in Stecca, B. & Zambelli, D. Analisi non standard 2015, docplayer.it) utilizzando infiniti e infinitesimi e definisce l’insieme dei numeri iperreali, le operazioni e le proprietà
- 03 – calcolo differenziale: di nuovo, si parte da problemi di geometria analitica e di fisica le cui soluzioni proposte fanno uso degli iperreali fino ad arrivare alla definizione di rapporto differenziale e di derivata, si analizza, con l’aiuto di GeoGebra, il grafico di una funzione in rapporto a quello della sua derivata
- 04 – derivata: si deducono le formule per alcune derivate fondamentali (polinomi, razionali fratte e irrazionali), e le principali formule di derivazione, compresa la formula per la derivata di una funzione composta
- 05 – applicazioni delle derivate: problemi che si possono risolvere usando le derivate (tangenti, velocità, accelerazione) e che non si possono risolvere con le derivate (tangente a una conica condotta per un pubnto esterno)
- 06 – ritorno a Hyperreal Mountain: la definizione del numero e utilizzando gli iperreali, derivate di funzioni logaritmiche ed esponenziali, alcuni esempi di comportamento asintotico
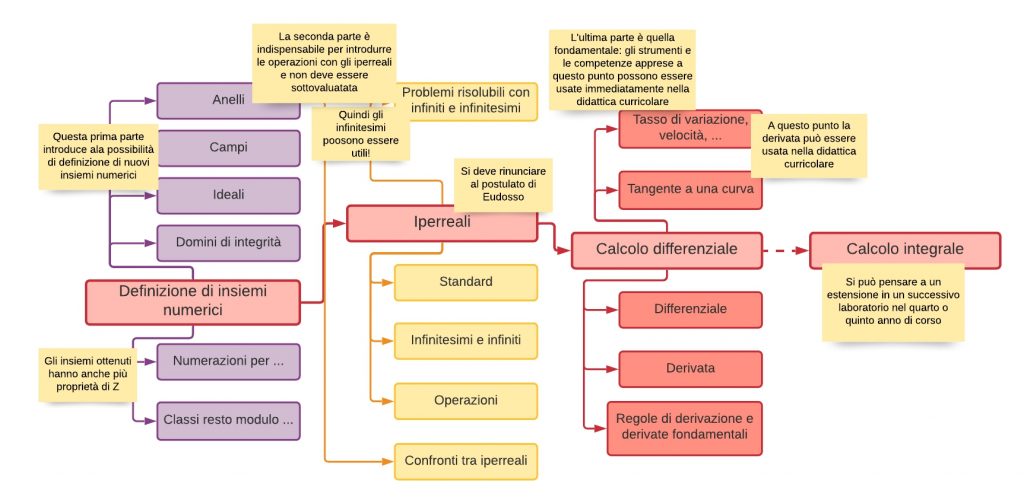
Obiettivi nel terzo anno del liceo scientifico
- Comprendere il concetto di derivata di una funzione reale
- Calcolare la derivata di funzioni polinomiali e irrazionali
- Calcolare la derivata di funzioni logaritmiche ed esponenziali
- Applicare la derivata a:
- problemi di geometri analitica (tangente a una curva, problemi di massimo
- e minimo, …)
- problemi di fisica (velocità e accelerazione, …)
- problemi di realtà (tasso di variazione, problemi di massimo e minimo, …)
- Dedurre le principali formule di derivazione (somma, prodotto,
- quoziente)
- Dedurre le derivate di alcune funzioni fondamentali (polinomi,
- funzioni irrazionali, …)
Bibliografia
- https://docplayer.it/AA.VV. Elementi di analisi non standard 2015, in Matematicamente (pubblicazione della sezione veronese di Mathesis)
- Goldoni, G. Il calcolo delle differenze e il calcolo differenziale 2014, Amazon fulfillment
- Goldoni, G. I numeri iperreali 2017, Ilmiolibro
- Robinson, A. Non standard analysis 1996, Priceton Univerity Press
- Stecca, B. & Zambelli, D. Analisi non standard 2015, docplayer.it
- Valenti, S. Dall’intero all’iperreale, un’introduzione graduata all’analisi non standard 1994, GRIM Quaderni di ricerca didattica n.5