A cura di Antonio Boscaro, Emanuele De Angelis, Delfo Galante, Matteo Giancristofaro, Gabriele MIlani. Questo articolo espande il laboratorio Il canale di circolazione.
I risultati ottenuti nel laboratorio Il canale di circolazione (qui potete trovare il fascicolo che descrive l’sperienza), in particolare la stima dell’errore che si può trovare a pagina 14 delle Soluzioni, ci permettono di affermare che le funzioni che abbiamo trovato approssimano molto bene i dati forniti. Ma, allontanandoci per un momento dalla matematica per dare un maggiore spazio alla fisica, queste riescono a descrivere bene il fenomeno nella sua interezza? Le variazioni di pressione e velocità rispetto a diversi valori di N e h0, sono plausibili? In questo articolo affronteremo queste domande, cercando di analizzare la teoria del fenomeno e vedendo se ci sono corrispondenze con le funzioni da noi trovate.
Il cuore dell’apparato sperimentale – il canale di circolazione – sta tutto nell’azione di una girante, che per l’appunto ruota spingendo l’acqua nella vasca. La girante è collegata ad un motore elettrico, e N è proprio proporzionale al numero di giri del motore. Cosa ci aspettiamo allora? Ci aspettiamo che quando il motore ha un numero di giri piuttosto piccolo la velocità dell’acqua nella vasca sia bassa mentre quando si aumenta la velocità di rotazione l’acqua attraversi la vasca più velocemente. Inoltre è chiaro che quando l’acqua nella vasca è poco profonda (quindi per valori di h0 piccoli), la velocità sarà maggiore rispetto a quando invece il livello nella vasca sarà alto.
Innanzitutto si deve tener conto dei limiti del problema, le funzioni trovate sono valide solo per valori di N compresi tra 0 e 40 mentre, ovviamente, h0 deve essere positivo e non superiore alla massima altezza possibile nella vasca. Chiariti questi limiti intrinseci al problema possiamo andare ad osservare se le funzioni trovate possano essere considerate corrette!
Ricordiamo a chi ha già letto il fascicolo 23 – Il canale di circolazione che le due funzioni hanno l’aspetto che segue:
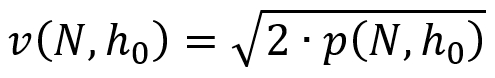
dove
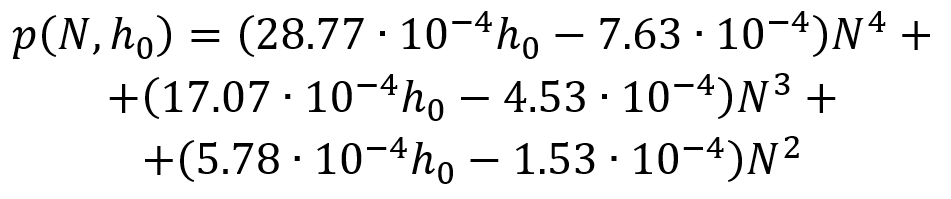
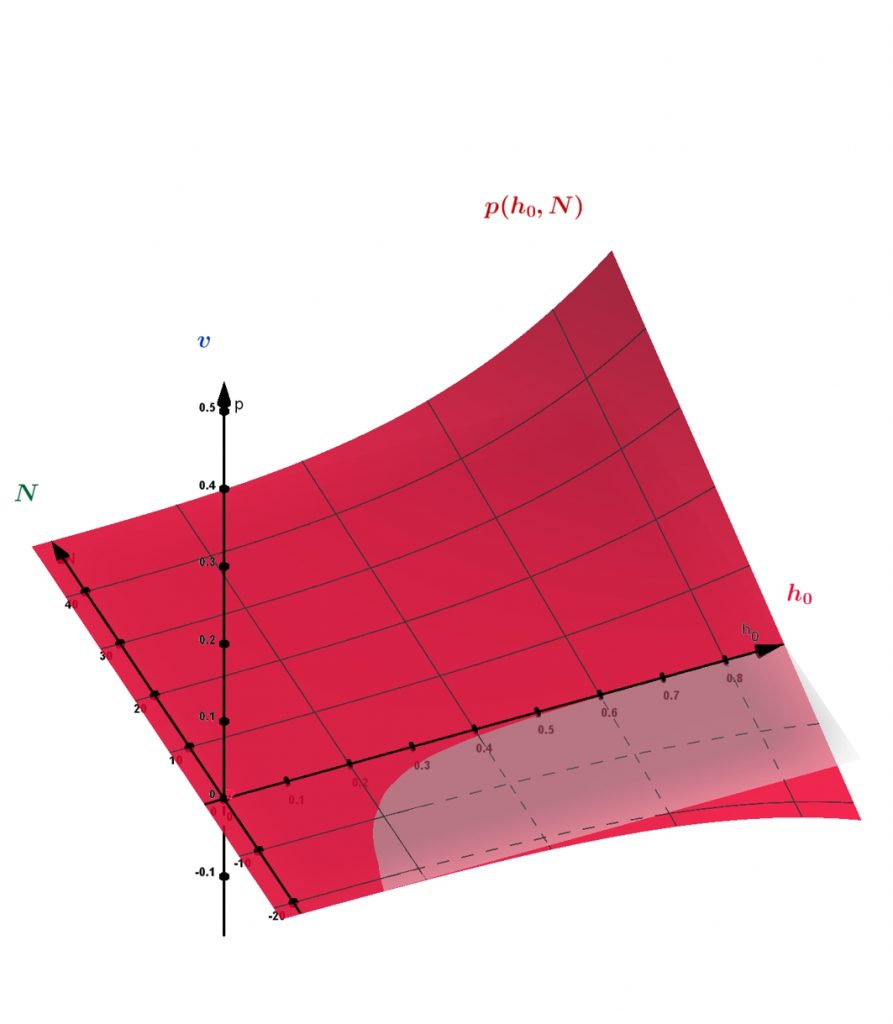
Qui a sinistra il grafico della funzione che approssima la pressione. Si nota subito che tende ad assumere valori molto bassi quando la girante è ferma o quasi (quindi con valori di N vicini a 0), ciò è dovuto dal semplice fatto che se il motore spinge poco, la pressione che eserciterà il liquido sarà ben poca. Per quanto riguarda invece valori più alti di N notiamo che la pressione tende ad aumentare, proprio come ci aspettavamo. Infatti sappiamo che il numero che appare sullo schermo dipende dalla velocità di rotazione del motore, dunque è direttamente proporzionale alla portata Q che non è altro che la velocità moltiplicata per la sezione di superficie S. Noi però sappiamo anche che la velocità è legata alla pressione (dal teorema di Bernoulli) ed è evidente che anche la pressione è direttamente legata alla portata:
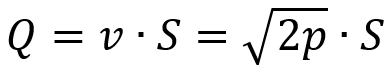
Dunque, in sintesi, se il il valore di N aumenta, anche la pressione dinamica aumenta.
Adesso però cerchiamo di guardare anche l’asse riguardante l’altezza dell’acqua. Notiamo con poco stupore che quando N è nullo, la pressione tende ad essere nulla per qualsiasi valore di h0: se il motore non gira non sposta acqua. Il dato curioso sta invece nella variazione della pressione quando N è fissato e cambia l’altezza, infatti risulta che la pressione tende a decrescere quando l’altezza aumenta. Questo fenomeno é spiegabile anche tramite un pratico esempio: se vogliamo spostare per esempio un divano e una sedia utilizzando la stessa intensità, noteremo quanto il divano, più pesante, si sposti di meno rispetto alla sedia. Dunque se vogliamo far muovere una massa d’acqua minima e una più grande con lo stesso numero di giri del motore, la prima assumerà un moto turbolento, la seconda invece si muoverà decisamente di meno.
Questo dato è da tenere in conto se si vuole per esempio fare una simulazione di un modello di nave su un fiume, dove l’acqua è poco profonda, o su mare, dove invece l’acqua sarà molto più profonda, per capire come reagirebbe la barca reale nelle diverse acque e con la stessa corrente. Per quanto riguarda la pressione dunque abbiamo trovato una spiegazione che riesce a dimostrare la validità della nostra funzione, ma per quella della velocità (che è quella effettivamente richiesta)?
Il ragionamento è molto simile, infatti ritornando alle leggi fisiche notiamo il legame particolare tra la velocità e la pressione. Utilizzando il teorema di Bernoulli e semplificando i vari valori costanti, notiamo che la velocità può essere ricavata facendo la radice quadrata del prodotto tra la pressione e la densità del fluido (che in questo caso, essendo acqua, è pari a circa 1). Dunque anche in questo caso la funzione è corretta, poiché le dipendenze da N e h0 sono simili.
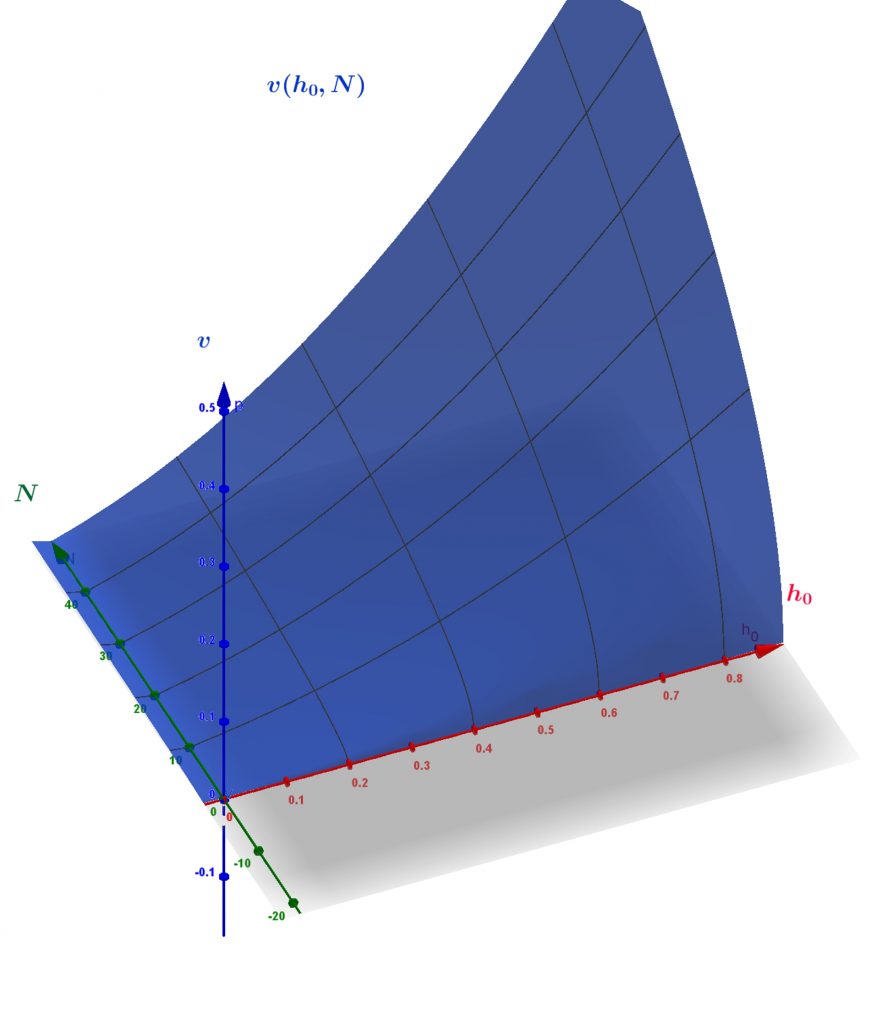
Volendo fare una piccola constatazione per confermare ancora di più a livello fisico la validità della nostra funzione, possiamo prendere l’esempio del divano e della sedia. Se per esempio per comodità sostituissimo i due oggetti con una palla da bowling (divano) e una biglia (sedia), applicando la stessa forza su entrambe noteremo che la biglia assumerà una velocità maggiore rispetto alla palla da bowling. Ancora una volta il concetto è simile alla nostra situazione, in cui però non varia l’oggetto ma solo la quantità di esso. Essendo poi N direttamente proporzionale alla portata Q, che ricordiamo essere il prodotto tra la velocità e la sezione della superficie, si spiega anche come fa ad aumentare la velocità con l’aumento del valore del numero che appare sul display.
Un’altra osservazione che possiamo fare sulle nostre due funzioni riguarda il valore massimo che si puó raggiungere di pressione o velocità. Infatti possiamo dire con certezza che il valore massimo che possono raggiungere le due funzioni si ottiene quando l’acqua nella vasca è poco profonda e il numero di giri del motore è alto. In quel caso però l’apparato – il canale di circolazione – produce un moto turbolento dell’acqua, che non risulta utile per le simulazioni a cui è destinato (a meno che non si voglia simulare l’andamento di una barchetta in una pozzanghera di acqua spinta dal vento).



