I laboratori sul Problema del postino cinese e il materiale didattico di supporto si trovano seguendo questo collegamento. Sul canale YouTube del progetto c’è una playlist dedicata a questo problema.
Il Problema del postino cinese è un classico dilemma della topologia e della teoria dei grafi. La sua formulazione, in termini non formali, è piuttosto semplice …
… ci si chiede come sia possibile per un postino consegnare la posta percorrendo tutte le strade di sua competenza una e una sola volta, ritrovandosi, alla fine del cammino di nuovo al punto di partenza.
Il problema però, in alcune situazioni, non è affatto banale e richiede una molteplicità di strumenti integrati tra loro per arrivare alla soluzione.
Nell’ambito del progetto, e pensando anche ai laboratori del liceo matematico, abbiamo costruito una serie di tre laboratori e relativi fascicoli per introdurre alla topologia e alla teoria dei grafi che, nell’ordine, sono: Quattro passi in centro, Un grafo connesso, Un problema di consegne. La struttura del laboratorio e il materiale didattico li trovate qui: Topologia e teoria dei grafi.
Nel seguito una breve introduzione (senza spoiler) a questi laboratori.
Un agevole esempio
In alcune situazioni il problema è davvero semplice, quasi banale. Seguite questo esempio facile, facile.
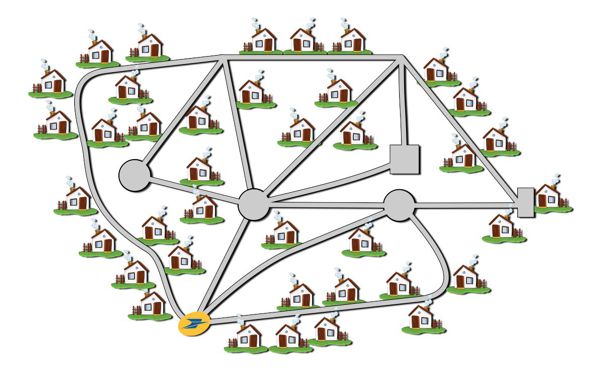
Per prima cosa costruiamo un modello per il nostro problema: rappresentiamo gli incroci con piccoli circoletti che chiameremo nodi e le vie con linee che collegano due nodi e che chiameremo archi, come mostrato nella figura qui sotto a sinistra. Quello che abbiamo costruito è un grafo: un modello per la situazione reale ma anche uno strumento sul quale lavorare per cercare la soluzione. State entrando nello stupefacente mondo della topologia!
Il problema era davvero facile perchè il grafo (e quindi il quartiere di competenza del postino) ha una particolare proprietà: da ogni incrocio parte un numero pari di strade. Perchè questa proprietà sia così importante e interessante è discusso nel laboratorio Quattro passi in centro.
Un esempio meno agevole
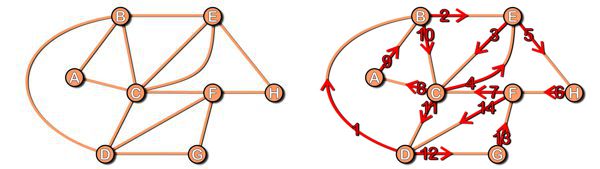
La situazione cambia di molto anche con pochissime modifiche alla situazione iniziale (la rete di collegamenti tra i nodi) ma c’è tutta una serie di casi in cui la soluzione, per quanto non scontata, si può trovare con una certa facilità.
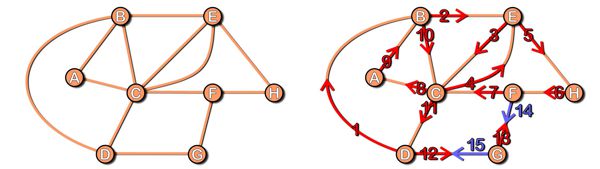
Poco male, il postino, una volta concluso il suo giro, deve perdere un po’ di tempo per tornare all’ufficio postale. Nella figura qui sopra, a destra, questo cammino a vuoto, nel corso del quale non si consegna la posta perché si attraversano strade già coperte in precedenza, è indicato in colore azzurro (in pratica, il postino conclude il suo giro nel nodo F e percorre gli archi da F a G e poi a D in modo da tornare al punto di partenza). Questa non è l’unica scelta possibile, per esempio avrebbe potuto percorrere la strada che da F porta a C e poi a D. Quale sia la scelta migliore è uno degli argomenti dibattuti nel laboratorio Un problema di consegne.
Un esempio per niente agevole
Ma la maggior parte dei casi reali non ricade in nessuna delle due categorie esemplificate in precedenza. Provate a dare un’occhiata a questo grafo …
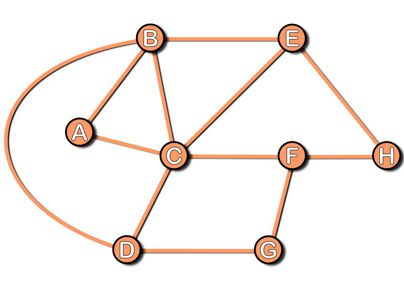
Vedrete ben presto che, malgrado i vostri tentativi, il problema sembra insolubile. È proprio in questi casi che il Problema del postino cinese si trasforma in una sfida avvincente, in una questione che richiede una strategia articolata e intrigante!


